Всё о метрологии
- Название:Всё о метрологии
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Всё о метрологии краткое содержание
Всё о метрологии - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Таблица 3
| 18.305 | 18.306 | 18.306 | 18.309 |
| 18.308 | 18.309 | 18.313 | 18.308 |
| 18.312 | 18.310 | 18.305 | 18.307 |
| 18.309 | 18.303 | 18.307 | 18.309 |
| 18.304 | 18.308 | 18.308 | 18.310 |
В качестве оценки математического ожидания длины детали принимаем ее среднее арифметическое
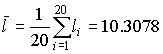 мм.
мм.
Точечная оценка среднеквадратического отклонения результатов наблюдений составляет:
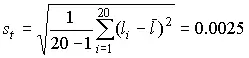 мм.
мм.
Приняв уровень доверительной вероятности α=1- q =0.90, находим для числа степеней свободы k = n –1 = 20–1 = 19 в табл. П.6 приложения:
χ² k ,0.5 q = χ² 19,0.05 = 10.117, χ 19,0.05 = 3.18,
χ² k ,1-0.5 q = χ² 19,0.95 = 30.144, χ 19,0.95 = 5.49.
Границы доверительного интервала для среднеквадратического отклонения результатов наблюдений находим по формуле (47):
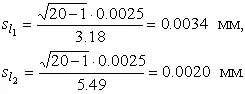
Полученные результаты говорят о том, что истинное значение среднеквадратического отклонения результатов наблюдений с вероятностью 0.90 лежит в интервале 0.0020–0.0034 мм.
В табл. П.6 приведены значения χ² k только при числах степеней свободы от 1 до 30. При k >30 можно пользоваться приближенной формулой
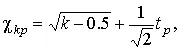
где t p определяется из условия Φ( t p )= P по табл. П.3, в которой помещены значения интегральной функции нормированного нормального распределения.
Тогда границы доверительного интервала для среднеквадратического отклонения результатов наблюдений при доверительной вероятности α=1- q вычисляются по формулам (47) при значениях χ k , равных
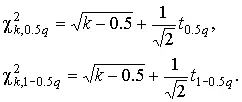 (49)
(49)
Так, если в условиях предыдущей задачи среднеквадратическое отклонение определено на основании n =42 измерений, то для α=1- q =0.90 из табл. П.3 находим:
t 0.5 q = t 0.05= –1,6449, t 1-0.5 q = t 0.95= +1,6449.
Величины χ k при k=n –1=41 составляют:
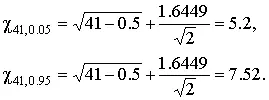
Границы доверительного интервала:
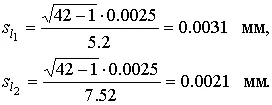
4.7. Проверка нормальности распределения результатов наблюдений
В предыдущих разделах было показано, что результаты наблюдений можно оценить наиболее полно, если их распределение является нормальным. Поэтому исключительно важную роль при обработке результатов наблюдений играет проверка нормальности распределения.
Эта задача представляет собой частный случай более общей проблемы, заключающейся в подборе теоретической функции распределения, в некотором смысле наилучшим образом согласующейся с опытными данными.
При большом числе результатов наблюдений ( n >40) данная задача решается в следующем порядке.
Весь диапазон полученных результатов наблюдений X max… X minразделяют на r интервалов шириной Δ X i (i=1,2,… r ) и подсчитывают частоты m i , равные числу результатов, лежащих в каждом i -м интервале, т. е. меньших или равных его правой и больших левой границы.
Отношения
 (50)
(50)
где n — общее число наблюдений, называются частостями и представляют собой статистические оценки вероятностей попадания результата наблюдений в i -й интервал. Распределение частот по интервалам образует статистическое распределение результатов наблюдений .
Если теперь разделить частость на длину интервала, то получим величины
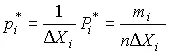 (51)
(51)
являющиеся оценками средней плотности распределения в интервале Δ X i .
Отложим вдоль оси результатов наблюдений (рис. 11) интервалы Δ X i в порядке возрастания индекса i и на каждом интервале построим прямоугольник с высотой, равной p i *. Полученный график называется гистограммой статистического распределения.

Площадь суммы всех прямоугольников равна единице:
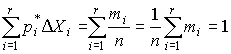
При увеличении числа наблюдений число интервалов можно увеличить. Сами интервалы уменьшаются, и гистограмма все больше приближается к плавной кривой, ограничивающей единичную площадь, — к графику плотности распределения результатов наблюдений.
При построении гистограмм рекомендуется пользоваться следующими правилами:
1. Число интервалов выбирается в зависимости от числа наблюдений согласно рекомендациям табл.6.
Таблица 6
| n | r |
|---|---|
| 40–100 | 7–9 |
| 100–500 | 8–12 |
| 500–1000 | 10–16 |
| 1000–10000 | 12–22 |
2. Длины интервалов удобнее выбирать одинаковыми. Однако если распределение крайне неравномерно, то в области максимальной концентрации результатов наблюдений следует выбирать более узкие интервалы.
3. Масштабы по осям гистограммы должны быть такими, чтобы отношение ее высоты к основанию составляло примерно 5÷8.
Пример.Было выполнено 100 измерений среднего диаметра резьбового калибра. Результаты наблюдений лежат в диапазоне 8.911–8.927 мм, т. е. зона распределения результатов составляет 0.016 мм. Весь диапазон удобно разделить на восемь равных интервалов через 0.002 мм. В табл. 7 приведены частоты m i , частости P i * и плотности p * статистического распределения.
Таблица 7
| i | X i , мм | X i +1, мм | m i | P i * | p i *, 1/мм |
|---|---|---|---|---|---|
| 1 | 8.911 | 8.913 | 1 | 0.01 | 5 |
| 2 | 8.913 | 8.915 | 5 | 0.05 | 25 |
| 3 | 8.915 | 8.917 | 14 | 0.14 | 70 |
| 4 | 8.917 | 8.919 | 27 | 0.27 | 13 |
| 5 | 8.919 | 8.921 | 24 | 0.24 | 120 |
| 6 | 8.921 | 8.923 | 18 | 0.18 | 90 |
| 7 | 8.923 | 8.925 | 9 | 0.09 | 45 |
| 8 | 8.925 | 8.927 | 2 | 0.02 | 10 |
После построения гистограммы надо подобрать теоретическую плавную кривую распределения, которая, выражая все существенные черты статистического распределения, сглаживала бы все случайности, связанные с недостаточным объемом экспериментальных данных. Принципиальный вид теоретической кривой выбирают заранее, проанализировав метод измерения, или хотя бы по внешнему виду гистограммы. Тогда определение аналитического вида кривой распределения сводится к выбору таких значений его параметров, при которых достигается наибольшее соответствие между теоретическим и статистическим распределением. Одним из методов решения этой задачи является метод моментов . При его использовании параметрам теоретического распределения придают такие значения, при которых несколько важнейших моментов совпадают с их статистическими оценками. Так, если статистическое распределение, определяемое гистограммой, приведенной на рис. 11, мы хотим описать кривой нормального распределения, то естественно потребовать, чтобы математическое ожидание и дисперсия последнего совпадали со средним арифметическим и оценкой дисперсий, вычисленным по опытным данным. В предыдущем примере 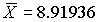 мм, s X =0.0028 мм и уравнение кривой нормального распределения, лучше всего согласующегося со статистическим распределением, должно иметь вид:
мм, s X =0.0028 мм и уравнение кривой нормального распределения, лучше всего согласующегося со статистическим распределением, должно иметь вид:
Интервал:
Закладка:







