Всё о метрологии

Таким образом, с помощью распределения Стьюдента по формуле (41) может быть найдена вероятность того, что отклонение среднего арифметического от истинного значения измеряемой величины не превышает 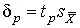, например 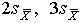и т.д. Итог измерений записывается в виде

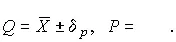(42)

Пример. По результатам пяти наблюдений была найдена длина стержня. Итог измерений составляет L =15.785 мм, 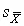=0.005 мм, причем существуют достаточно обоснованные предположения о том, что распределение результатов наблюдений было нормальным. Требуется оценить вероятность того, что истинное значение длины стержня отличается от среднего арифметического из пяти наблюдений не больше чем на 0.01 мм.

Из условия задачи следует, что имеются все основания для применения распределения Стьюдента.

Вычисляем значение дроби Стьюдента

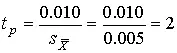
и число степеней свободы

k = n –1 = 5–1 = 4.

По данным табл. П.4 приложения находим значение доверительной вероятности для

t p = 2 и k = 4: .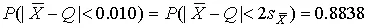

Для t p = 3 вероятность составляет

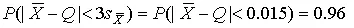
т.е несколько меньше 0.9973, как при нормальном распределении. Итог измерений удобно записать в виде

L = (15.785±0.010) мм, P = 0.8838.

Для t p = 1 доверительная вероятность составляет приблизительно 0.62, поэтому итог измерений можно представить также в виде

L = (15.785±0.005) мм, P = 0.62,

L = (15.785±0.015) мм, P = 0.96.

Пример.В условиях предыдущей задачи найти доверительную границу погрешности результата измерений для доверительной вероятности P =0.99. По данным табл. П.5 при k =4 находим t p =4.604 и, следовательно, доверительная граница:

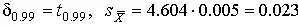мм.

Итог измерений:

L = (15.785±0.023) мм, P = 0.99.

При n →∞, а практически уже при n = 20–30 распределение Стьюдента переходит в нормальное распределение и

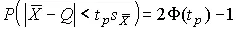
где Φ( t p ) — интегральная функции нормированного нормального распределения.

В тех случаях, когда распределение случайных погрешностей не является нормальным, все же часто пользуются распределением Стьюдента с приближением, степень которого остается неизвестной.

Кроме того, на основании центральной предельной теоремы теории вероятностей можно утверждать, что при достаточно большом числе наблюдений распределение среднего арифметического как суммы случайных величин X i / n будет сколь угодно близким к нормальному. Тогда, заменяя дисперсию σ² X ее точечной оценкой [см. п. 4.4. Нормальное распределение], можно для оценки доверительной границы погрешности результата воспользоваться равенством (35). Число наблюдений n , при котором это становится возможным, зависит, конечно, от распределения случайных погрешностей.

Соотношения (38) показывают, что итог измерения не есть одно определенное число. В результате измерений мы получаем лишь полосу значений измеряемой величины. Смысл итога измерений, например, L =20.00±0.05 заключается не в том, что L = 20.00, как для простоты считают, а в том, что истинное значение лежит где-то в границах от 19.95 до 20.05. К тому же нахождение внутри границ имеет некоторую вероятность, меньшую, чем единица, и, следовательно, нахождение вне границ не исключено, хотя и может быть очень маловероятным.

Теперь найдем доверительные интервалы для дисперсии и среднеквадратического отклонения результатов наблюдений.

Если распределение результатов наблюдений нормально, то отношение

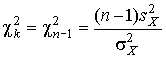(43)

имеет так называемое χ²-распределение Пирсона с k=n –1 степенями свободы. Его дифференциальная функция распределения описывается формулой

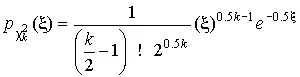(44)

Кривые плотности χ²-распределения при различных значениях k , вычисленные по формуле (44), представлены на рис. 9.

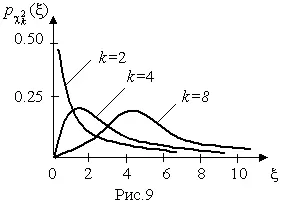
Значения χ² kp , соответствующие различным вероятностям Р того, что отношение (43) в данном опыте будет меньше χ² kp , представлены в табл. П.6 приложения для различных вероятностей Р и чисел k степеней свободы.

Пользуясь этой таблицей, можно найти доверительный интервал для оценки дисперсии результатов наблюдений при заданной доверительной вероятности. Этот интервал строится таким образом, чтобы вероятность выхода дисперсии за его границы не превышала некоторой малой величины q , причем вероятности выхода за обе границы интервала были бы равны между собой и составляли соответственно q /2 (рис.10).

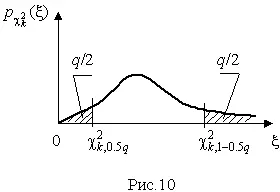
Границы χ² k ,0.5 q и χ² k ,1–0.5 q такого доверительного интервала находят из равенства

F(χ² k ,0.5 q ) = 0.5q, F(χ² k ,1-0.5 q ) = 1-0.5q (45)

Теперь, зная границы доверительного интервала для отношения χ² kp , запишем доверительный интервал для дисперсии:

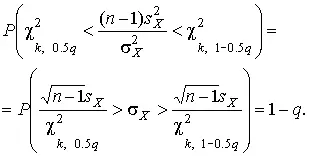(46)

Полученное равенство означает, что с вероятностью α=1- q истинное значение σ X среднеквадратического отклонения результатов наблюдений лежит в интервале ( 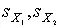], границы которого равны

(47)

Пример.Даны результаты двадцати измерений длины l i мм детали (табл.3).