Всё о метрологии
- Название:Всё о метрологии
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Всё о метрологии краткое содержание
Всё о метрологии - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Если же об исходных распределениях нет никаких заслуживающих внимания данных, то на основании центральной предельной теоремы можно все-таки предполагать, что распределение среднего взвешенного нормально, поскольку оно является суммой большого числа случайных величин с конечными дисперсиями и математическими ожиданиями.
Пример.Тремя коллективами экспериментаторов с помощью различных методов измерения были получены следующие значения ускорения свободного падения (со среднеквадратическими отклонениями результатов измерений):
g =(981.9190±0.0004) смˉ²;
g =(981.9215±0.0016) смˉ²;
g =(981.9230±0.0020) смˉ²;
Весовые коэффициенты отдельных результатов вычислим по формуле (68):
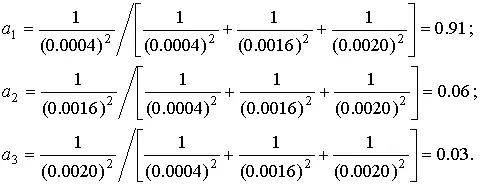
Среднее взвешенное в соответствии с уравнением (69) составляет:

и его дисперсия (70)
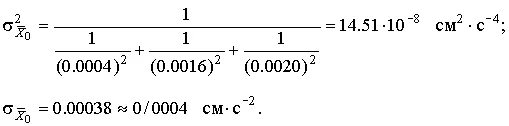
6.3. Обработка результатов косвенных измерений
При косвенных измерениях значение искомой величины получают на основании известной зависимости, связывающей ее с другими величинами, подвергаемыми прямым измерениям.
Вначале рассмотрим тот простейший случай, когда искомая величина Q Z определяется как сумма двух величин Q X и Q Y :
Q Z = Q X + Q Y (72)
Поскольку результаты прямых измерений величин Q X и Q Y (после исключения систематических погрешностей) включают в себя некоторые случайные погрешности, то формулу косвенного измерения суммы можно переписать в виде
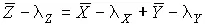 , (73)
, (73)
где 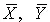 — средние арифметические (или средние взвешенные), полученные при обработке результатов прямых измерений величин Q X и Q Y , λ X и λ Y — случайные погрешности средних,
— средние арифметические (или средние взвешенные), полученные при обработке результатов прямых измерений величин Q X и Q Y , λ X и λ Y — случайные погрешности средних, 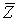 и λ Z — оценка истинного значения косвенно измеряемой величины и его случайная погрешность.
и λ Z — оценка истинного значения косвенно измеряемой величины и его случайная погрешность.
Из уравнения (73) непосредственно вытекает справедливость двух следующих равенств:
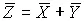 , λ Z = λ X – λ Y , (74)
, λ Z = λ X – λ Y , (74)
т.е. оценкой истинного значения косвенно измеряемой величины должна служить сумма оценок истинных значений исходных величин, случайные погрешности которых складываются.
Математическое ожидание оценки 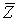 равно, очевидно, истинному значению искомой величины:
равно, очевидно, истинному значению искомой величины:
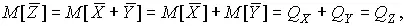
а ее дисперсия:
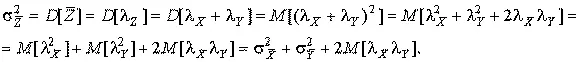
Входящее в это выражение математическое ожидание произведения случайных погрешностей называется корреляционным моментом и определяет степень “тесноты” линейной зависимости между погрешностями. Вместо корреляционного момента часто пользуются безразмерной величиной, называемой коэффициентом корреляции:
 . (75)
. (75)
Отсюда, в частности, следует, что коэффициент корреляции между погрешностями λ X и λ Y средних арифметических равен коэффициенту корреляции между погрешностями δ X и δ Y результатов отдельных измерений величин Q X и Q Y : 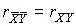 .
.
С учетом коэффициента корреляции дисперсия результата косвенных измерений, т. е. оценки истинного значения косвенно измеряемой величины,
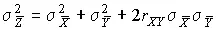 . (76)
. (76)
Если погрешности измерения величин Q X и Q Y не коррелированы, то выражение (76) упрощается:
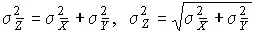 . (77)
. (77)
В тех случаях, когда теоретические дисперсии распределения результатов прямых измерений неизвестны, определяется оценка 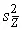 дисперсии результата косвенных измерений через оценки дисперсий
дисперсии результата косвенных измерений через оценки дисперсий 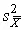 и
и 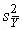 :
:
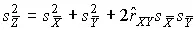 . (78)
. (78)
Оценки коэффициента корреляции 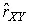 вычисляют на основании результатов прямых измерений исходных величин:
вычисляют на основании результатов прямых измерений исходных величин:
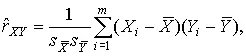 (79)
(79)
m = min( n X , n Y ) — наименьшее из чисел наблюдений n X и n Y .
При положительной корреляции, т. е. когда r XY > 0, одна из погрешностей имеет тенденцию возрастать при увеличении другой, если же корреляция отрицательна, то r XY < 0 и погрешность измерения одной величины обнаруживает тенденцию к уменьшению при увеличении погрешности измерения другой величины. Возможные значения коэффициента корреляции лежат в интервале –1 < r XY < +1. Если r XY = 0, то погрешности измерения некоррелированы.
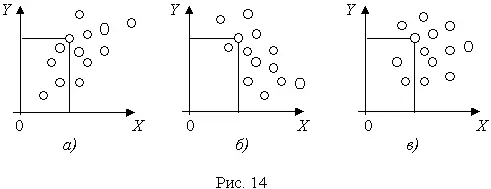
О наличии корреляции удобно судить по графику, на котором в координатах X, Y изображены пары последовательно получаемых результатов измерения величин Q X и Q Y .
На рис.14 изображены случаи совместного распределения результатов измерения при положительной (рис. 14, а ) и отрицательной (рис. 14, б ) корреляции. Результаты измерений на рис. 15, в некоррелированы.
Чаще всего наличия корреляции следует ожидать в тех случаях, когда обе величины измеряются одновременно однотипными измерительными средствами, причем неуловимые изменения внешних воздействий (электрических, магнитных, температурных и других полей, условий питания) одновременно заметно влияют на формирование случайных погрешностей их измерения. В некоторых случаях причиной корреляции между результатами измерений может стать сам оператор, поскольку при некоторых исследованиях, связанных с ручным уравновешиванием приборов сравнения (сличением мер на точных весах, в фотометрии), искусство и опыт наблюдателя оказывают значительное влияние на результаты измерений. В тех же случаях, когда исходные величины измеряют с помощью различных средств измерения в разное время, можно с полным правом ожидать, что результаты, если и будут коррелированы, то очень мало, и коэффициентом корреляции в выражениях (76) и (78) можно пренебречь.
Читать дальшеИнтервал:
Закладка:







