Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

Помимо активной помощи в борьбе с эпидемиями, математические модели эпидемий также могут объяснить необычные закономерности, свойственные различным заболеваниям. Так, ряд интересных вопросов сформировался вокруг детских болезней, таких как свинка и краснуха: почему их периодические вспышки поражают только детей? Возможно, предрасположенность к ним обусловлена каким-то до сих пор неизвестным свойством, присущим только детям? И почему эти болезни так долго сохраняются в нашем обществе? Может, они, словно в засаде, годами находятся в латентном состоянии, выбирая время для того, чтобы обрушиться на самых беззащитных?

Причина, по которой для детских заболеваний характерны периодические вспышки, заключается в том, что значение реального коэффициента репродукции с течением времени варьируется в зависимости от популяции восприимчивых к ним лиц. После того как крупная вспышка той же скарлатины поразит значительную часть незащищенной популяции детей, она не просто исчезает. Она сохраняется в популяции, но ее реальный коэффициент репродукции колеблется в районе единицы. Болезнь только поддерживает себя. Со временем население стареет, и рождаются новые, незащищенные дети. По мере роста незащищенной части популяции реальный коэффициент репродукции растет, что увеличивает вероятность новых вспышек. Когда болезнь наконец начинает распространяться, ее жертвы, как правило, принадлежат к незащищенному молодому поколению, поскольку большинство пожилых людей уже иммунизированы – ведь они столкнулись с этой болезнью раньше. Те же, кто не переболел скарлатиной в детстве, как правило, получают определенную степень защиты от нее, поскольку они меньше общаются с представителями инфицированной возрастной группы.

Концепция, что большое количество людей с иммунитетом может замедлить или даже остановить распространение инфекции, как это происходит в периоды покоя между вспышками детских болезней, на математическом языке называется популяционным иммунитетом [197]. Как ни странно, для работы этому эффекту общества не нужно, чтобы от заболевания были защищены все. Опустив значение реального коэффициента репродукции ниже единицы, можно разорвать цепь передачи инфекции и остановить распространение болезни. Популяционный иммунитет предполагает, что обеспеченная вакцинацией защита в некоторой мере распространяется и на тех, у кого иммунная система слишком слаба, чтобы переносить прививки (включая пожилых, новорожденных, беременных женщин и людей с ВИЧ). Это исключительно важно. Пороговое значение величины иммунной части населения, необходимое для защиты его восприимчивой части, варьируется в зависимости от того, насколько заболевание заразно. Ключом к тому, насколько эта доля велика, является базовый показатель репродукции R 0.

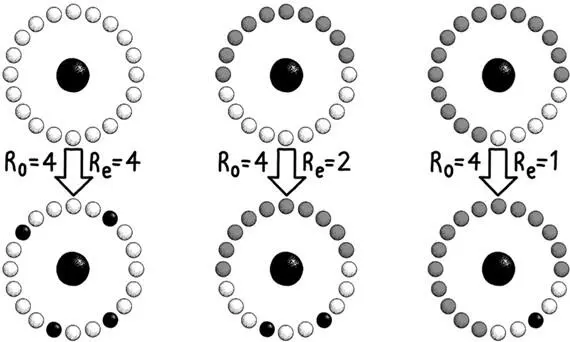
Рис. 24. Один инфицированный (черный круг) сталкивается с 20 восприимчивыми (белый круг) или вакцинированными (серый круг) лицами в течение недельного инфекционного периода. Если не вакцинирован никто (слева), один заразившийся заражает четырех других, т. е. базовый показатель репродукции R 0равен 4. При вакцинировании половины населения (в середине) заражаются только двое восприимчивых. Реальный коэффициент репродукции, R e, уменьшается до 2. Наконец, когда вакцинировано 3/4 населения (справа), в среднем заражается только один человек. Реальный коэффициент репродукции снижается до критического значения 1

Возьмем, к примеру, человека, зараженного вирулентным штаммом гриппа. Если за неделю, столкнувшись с 20 восприимчивыми к вирусу людьми, он заразит четверых из них, то значение базового показателя репродукции заболевания R 0составит 4. У каждого восприимчивого человека шанс заразиться составляет один к пяти. Это демонстрирует, как показатель репродукции зависит от размера восприимчивой популяции. Если бы наш больной гриппом в течение недели, во время которой он остается носителем вируса, встречался только с десятью восприимчивыми к инфекции людьми (как на средней схеме на рис. 24), то при той же вероятности передачи он заразил бы в среднем только двоих, понизив реальный коэффициент репродукции вдвое – с 4 до 2.

Наиболее эффективный способ сокращения численности восприимчивого населения – вакцинация. Количество человек, которых нужно вакцинировать для достижения популяционного иммунитета, определяется задачей сделать реальный коэффициент репродукции ниже единицы. Если бы мы смогли вакцинировать 3/4 популяции, то (как в схеме справа на рис. 24) из первоначальных 20 контактов нашего больного гриппом, только 1/4 (то есть пятеро) все равно были бы восприимчивы к инфекции. Из них в среднем заразился бы только один. Неслучайно этот критический порог вакцинации для достижения популяционного иммунитета к заболеванию с базовым показателем репродукции 4 требует вакцинации трех четвертей (то есть 1 минус 1/4) населения. В целом для достижения порога коллективного иммунитета мы можем позволить себе оставить 1/R 0популяции без вакцинации и должны защитить ее оставшуюся долю (1 минус 1/R 0популяции). При оспе, базовый показатель репродукции которой составляет около 4, мы можем позволить себе оставить четверть (то есть 25 %) популяции незащищенной. Вакцинации 80 % (на 5 % выше 75-процентного критического порога иммунизации для обеспечения буфера) восприимчивого к оспе населения в 1977 году хватило для того, чтобы совершить одно из величайших достижений нашего вида – стереть одну из человеческих болезней с лица Земли. Повторить этот подвиг не удалось.

Изнурительные и опасные последствия оспы сами по себе сделали ее подходящей мишенью для искоренения. Низкий критический порог иммунизации сделал ее еще и относительно легкой мишенью. От многих других болезней защититься сложнее, так как они распространяются легче. Ветряная оспа, с оценочным R 0около 10, для эффективной защиты всего человечества – и последующего искоренения болезни потребовала бы иммунизировать 9/10 населения Земли. Корь – безусловно, самая заразная болезнь человека на Земле, с оценочным R 0от 12 до 18 – потребует вакцинации от 92 до 95 % населения. Исследование, смоделировавшее распространение вспышки кори в Диснейленде в 2015 году, в ходе которой заразился Мёбиус Луп, позволило предположить, что уровень вакцинирования среди лиц, подверженных этому заболеванию, мог составлять до 50 % – намного ниже порога, необходимого для обеспечения популяционного иммунитета [198].

С момента введения в 1988 году в Англии вакцинирования против кори с помощью комбинированной прививки кори, свинки и краснухи (MMR [199]) ее масштаб неуклонно рос. В 1996 году уровень вакцинирования достиг рекордно высокой отметки в 91,8 %, что близко к критическому порогу иммунизации для ликвидации кори. Затем, в 1998 году, произошло нечто, что могло бы подорвать процесс иммунизации на многие годы.