Пол Стейнхардт - Невозможность второго рода. Невероятные поиски новой формы вещества

Для нас с Довом это был поистине захватывающий момент. Теперь мы точно знали, что находимся на пути к открытию, которое прямо противоречит столетним теоремам Гаюи и Браве. Мы были уверены, что линии Амманна таят в себе ключ к обходу этих надежно доказанных теорем и к объяснению секрета симметрии замощений Пенроуза. Но нам еще только предстояло расшифровать их смысл.

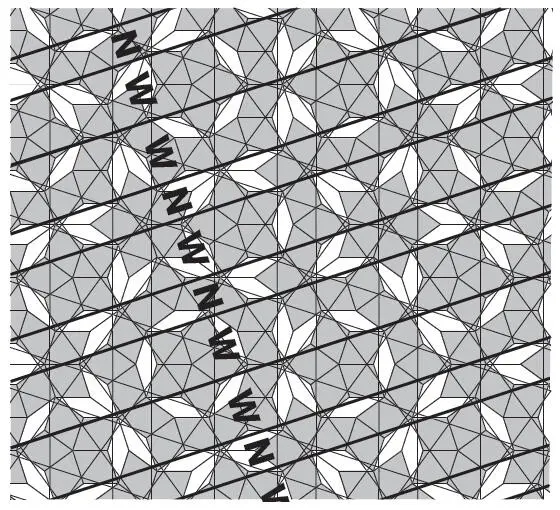
Важнее всего оказалось сосредоточиться лишь на одном из пяти наборов прямых линий, например на том, который выделен на рисунке справа. Видно, что просветы между этими параллельными линиями Амманна бывают двух размеров – широкие (W) и узкие (N). Для нас самыми важными были две величины: отношение между ширинами этих двух типов просветов и частота, с которой они повторяются на рисунке. Мы были на пороге открытия того, что эти две величины – отношение и последовательность – связаны с двумя знаменитыми математическими понятиями: золотым сечением и числами Фибоначчи.

Золотое сечение часто обнаруживается в природе и с древних времен встречается в искусстве. Считается, что египтяне руководствовались им при строительстве великих пирамид. В V веке до нашей эры греческий скульптор и математик Фидий утверждал, что применял золотое сечение при создании Парфенона в Афинах, который сегодня считается величайшим памятником греческой цивилизации. В память о Фидии это отношение часто обозначают греческой буквой Φ (произносится как “фи”).

Греческому математику Евклиду, которого считают отцом геометрии, принадлежит самое раннее сохранившееся определение золотого сечения с использованием простых объектов. Он рассматривал способы разделить палку на две части таким образом, чтобы соотношение короткого и длинного кусков было равно соотношению длинного и их суммарной длины. Найденное Евклидом решение состоит в том, что более длинный кусок должен быть ровно в Φ раз больше короткого, где Φ равно

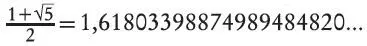
и выражается бесконечной неповторяющейся последовательностью десятичных цифр.

Числа, представляемые бесконечными непериодическими десятичными дробями, называются иррациональными, поскольку их нельзя выразить отношением двух целых чисел. Это отличает их от рациональных чисел, таких как 1/3 или 143/548, которые представляют собой отношения целых чисел и в десятичной форме записываются как 0,333… и 0,26094890510948905109… соответственно, то есть содержат периодически повторяющиеся последовательности цифр, если вычислить достаточное их количество.

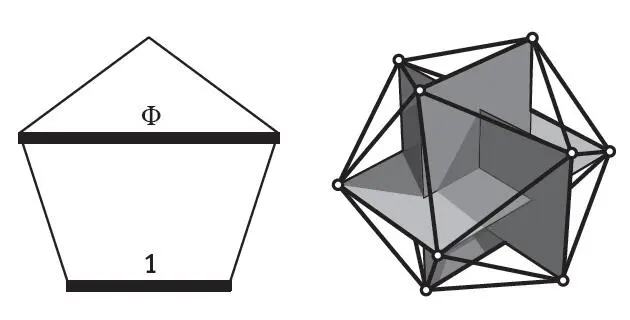
Впрочем, появление золотого сечения в симметрии пятого порядка в замощении Пенроуза не то чтобы сильно поразило нас с Довом, поскольку это соотношение напрямую связано с геометрией пятиугольника. Например, на левом рисунке внизу отношение длины верхнего отрезка, соединяющего противоположные вершины пятиугольника, к длине одной из его сторон равно золотому сечению. Икосаэдр, изображенный справа, также заключает в себе золотое сечение: его двенадцать вершин образуют три взаимно перпендикулярных прямоугольника, у каждого из которых отношение длины к ширине равно золотому сечению.

По-настоящему удивило нас с Довом то, что мы обнаружили золотое сечение также и в чередовании широких (W) и узких (N) просветов.

Рассмотрим последовательность просветов W и N на рисунке со страницы 71. В ней нет никакого регулярного повторения. Если вы станете подсчитывать количество W и N, следя за соотношением этих чисел, то после учета первых трех просветов получите отношение 2 к 1, после первых пяти – 3 к 2, после первых восьми – 5 к 3 и так далее.

Есть простое арифметическое правило, которое порождает эту последовательность. Возьмем первое отношение – 2 к 1. Сложим эти два числа (2 + 1 = 3) и затем сравним сумму (3) с большим из двух исходных чисел (2). Получится новое отношение – 3 к 2, которое также оказывается очередным в последовательности, полученной для просветов. Сложим следующие два числа (3 + 2 = 5) и снова сравним результат с большим из двух предыдущих чисел – получим отношение 5 к 3.

Этот процесс можно продолжать бесконечно, получая соотношения 8 к 5, 13 к 8, 21 к 13, 34 к 21, 55 к 34 и так далее. Эти соотношения будут в точности предсказывать последовательность для амманновских просветов.

Мы с Довом сразу узнали эту последовательность целых чисел: 1, 2, 3, 5, 8, 13, 21, 34, 55, … Она известна как числа Фибоначчи и названа в честь итальянского математика Леонардо Фибоначчи, жившего в Пизе в XIII веке.

Отношения последовательных чисел Фибоначчи – 2:1, 3:2, 5:3, … – это отношения целых чисел, а значит, они рациональные. Однако знаменитое свойство последовательности Фибоначчи состоит в том, что чем больше становятся целые числа, тем ближе их отношение подходит к золотому сечению. Такова его связь с числами Фибоначчи.

Как оказалось, единственный способ получить такое чередование W и N, которое воспроизводит числа Фибоначчи, состоит в том, чтобы по мере распространения замощения Пенроуза по всем направлениям просветы W повторялись с большей частотой, чем N, в соотношении, в точности равном золотому сечению – иррациональному числу. Если коротко, то именно в этом и состоит секрет замощения Пенроуза.

Последовательность, состоящая из двух элементов, повторяющихся с разными частотами, отношение которых выражается иррациональным числом, называется квазипериодической . Квазипериодическая последовательность никогда не повторяется в точности.

Например, нет таких двух просветов в последовательности Фибоначчи, которые были бы окружены одинаково расположенными наборами просветов с ширинами W и N, хотя в некоторых случаях надо зайти достаточно далеко, чтобы обнаружить различия. То же относится и к плиткам Пенроуза. Отследите замощение достаточно далеко, и вы обнаружите, что никакие две плитки не будут окружены в точности одинаковой конфигурацией других.

Наконец-то мы с Довом поняли, где именно пролегает путь в обход вековых правил Гаюи и Браве. Фундаментальная теорема кристаллографии гласит: если схема расположения плиток или атомов является периодической , повторяющейся с одной определенной частотой, то возможны только некоторые симметрии. В частности, симметрия пятого порядка по любому направлению совершенно невозможна для периодических конфигураций атомов. Тут следует говорить о невозможности первого рода, то есть об абсолютно непреложной истине, подобно тому как 1 + 1 ни при каких условиях не может дать 3.