Пол Стейнхардт - Невозможность второго рода. Невероятные поиски новой формы вещества

Не забывайте, что, согласно открытию Гаюи, кристаллы периодичны, подобно плитке на вашем полу с регулярно повторяющимся рисунком. Соответственно, те же ограничения, что применимы к замощениям, будут применимы и к трехмерным кристаллам. Лишь некоторые формы могут соединяться друг с другом, не оставляя зазоров.

Однако, несмотря на это сходство, трехмерные кристаллы намного сложнее плитки для пола, поскольку они могут иметь различные вращательные симметрии вдоль разных лучей зрения. Симметрии меняются в зависимости от точки, с которой наблюдается объект. Однако вне зависимости от направления взгляда для регулярно повторяющихся трехмерных структур и периодических кристаллов возможны только симметрии первого, второго, третьего, четвертого и шестого порядка – те же, что и для двумерных плиток. И с какой бы стороны вы ни смотрели на объект, вращательная симметрия пятого порядка всегда запрещена, так же как симметрии седьмого, восьмого и любого более высокого порядка.

Сколько различных сочетаний симметрий, наблюдаемых с разных направлений, может встретиться в периодических кристаллах? Поиск ответа на этот вопрос был серьезным испытанием для математической мысли.

Эта задача была окончательно решена в 1848 году французским физиком Огюстом Браве, который показал, что существует ровно 14 таких комбинаций. Сегодня они известны как “решетки Браве”.

Однако проблема понимания кристаллических симметрий этим не исчерпывалась. Позднее была разработана более полная математическая классификация, совмещающая вращательные симметрии с еще более сложными симметриями – “зеркальными”, “центральными” и “скользящими”. При объединении всех этих дополнительных вариантов общее число допустимых симметрий возрастает с 14 до 230. Однако даже при таком многообразии симметрия пятого порядка остается запрещенной для любых направлений.

В этих открытиях красота математики самым удивительным образом совмещается с красотой природного мира. Все эти 230 возможных трехмерных схем кристаллов [3] Строгий термин – “пространственные кристаллографические группы”. были найдены при помощи чистой математики. И каждый из этих рисунков был обнаружен в природе при раскалывании минералов.

Замечательное соответствие абстрактных, математических схем кристаллов и реальных, найденных в природе образцов было косвенным, но убедительным свидетельством в пользу того, что вещество состоит из атомов. Но как именно расположены эти атомы? Раскалывание кристаллов позволяет выяснить форму их строительных блоков, но этот метод слишком груб для определения того, как внутри них расположены атомы.

Точный инструмент, позволяющий получить эту информацию, был изобретен в 1912 году немецким физиком Максом фон Лауэ в Мюнхенском университете. Он обнаружил, что можно точно определить скрытую симметрию вещества, просто облучая небольшой образец рентгеновским пучком.

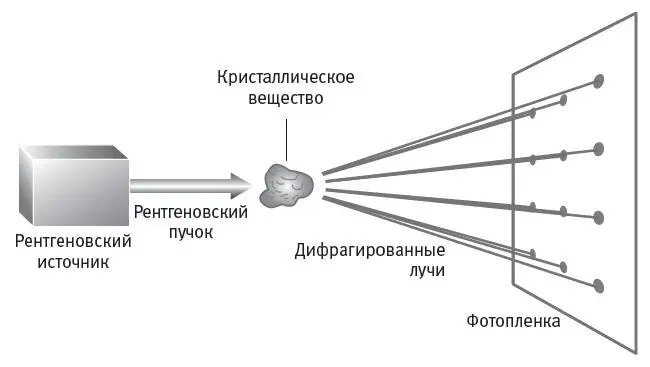
Рентгеновские лучи – это разновидность световых волн, длина которых настолько мала, что они легко проходят по каналам пустого пространства между регулярно расположенными рядами атомов в кристаллах. Когда рентгеновские лучи, прошедшие сквозь кристалл, попадают затем на фотобумагу, они, как показал фон Лауэ, интерферируют друг с другом, порождая характерный узор из четко очерченных точек, известный как рентгеновская дифракционная картина.

Когда рентгеновские лучи проходят по кристаллу вдоль оси его вращательной симметрии, получающийся узор из точек дифракционной картины обладает в точности такой же симметрией. Просвечивая кристалл рентгеновскими лучами с разных направлений, можно выявить весь набор симметрий его атомной структуры. А уже исходя из этих данных можно затем определить решетку Браве для кристалла и форму его строительных блоков.

Вскоре после открытия фон Лауэ еще один прорыв в этой области совершили британские физики Уильям Генри Брэгг и его сын Уильям Лоуренс Брэгг. Тщательно управляя длиной волны и направлением рентгеновских лучей, они показали, что по состоящей из точек дифракционной картине можно определить не только симметрию, но и конкретное расположение атомов внутри кристалла. Точки на этой дифракционной картине стали называть “брэгговскими пиками”.

Эти два прорывных метода сразу стали незаменимыми в исследованиях вещества. В последующие десятилетия по всему миру были получены десятки тысяч дифракционных картин различных природных и синтетических материалов. Позднее ученые стали получать еще более точную информацию, заменяя рентгеновские лучи электронами, нейтронами или высокоэнергичным излучением, которое порождается, когда пучок заряженных частиц, движущихся с релятивистскими скоростями, поворачивает под действием магнитов в синхротроне – мощном ускорителе элементарных частиц. Однако независимо от используемого метода исходные правила симметрии, выведенные в работах Гаюи и Браве, оставались непогрешимыми.

Эти правила, основанные на сочетании математических рассуждений и собранных экспериментальных результатов, надежно закрепились в сознании ученых. Тот факт, что вещество может обладать только рядом определенных, давно описанных симметрий, казался настолько надежно установленным, насколько вообще может быть надежен научный принцип.

И вот он я – стою перед Ричардом Фейнманом и объясняю ему, что эти давно установленные правила ошибочны.

Кристаллы оказались не единственной возможной формой вещества с упорядоченно расположенными атомами и точечными дифракционными картинами. Перед нами открывался целый новый мир возможностей со своими собственными правилами. Мир квазикристаллов.

Это название было выбрано нами, чтобы подчеркнуть принципиальное отличие этих материалов от обычных кристаллов. И те и другие состоят из групп атомов, которые повторяются по всему объему.

Группы атомов в кристаллах повторяются с регулярными интервалами, как в пяти рассмотренных выше схемах. В квазикристаллах, однако, разные группы повторяются с разными интервалами. Источником нашего вдохновения стал двумерный узор, известный как мозаика Пенроуза, представляющий собой необычное замощение из двух разных типов плиток, которые повторяются с двумя несоизмеримыми [4] Несоизмеримыми называют величины, отношение которых выражается иррациональным числом, как сторона и диагональ квадрата. интервалами. Математики называют такие замощения квазипериодическими. Поэтому мы назвали наше теоретическое открытие квазипериодическими кристаллами , или сокращенно квазикристаллами .