Наталья Ларионова - Олимпиадный физический минимум для семиклассника. Рабочая тетрадь

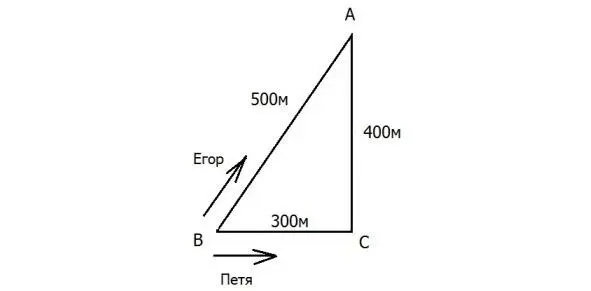
3. Два друга – Егор и Петя – устроили гонки на велосипедах вокруг квартала в дачном посёлке (см. рис.). Стартовав одновременно из точки В в разные стороны, Егор – вдоль улицы ВА, Петя – вдоль улиц ВС и СА, друзья встретились через 4 минуты в точке А и продолжили гонки с постоянными по модулю скоростями, объезжая квартал раз за разом в противоположных направлениях. Через какое минимальное время после этой встречи они снова окажутся вместе в точке А?

Задачи для самостоятельного решения

1. Мальчику разрешили погулять по лесу сорок пять минут. В течение 20 минут он шёл с постоянной скоростью на север, затем в течение 15 минут с той же скоростью шёл на запад. Вспомнив о времени прогулки, он поторопился вернуться назад и побежал по кратчайшему пути со скоростью в два раза большей, чем шёл до этого. Успеет ли мальчик вернуться к намеченному сроку?

2. Дельфин плывёт со скоростью 18 км/ч вдоль стенок квадратного бассейна, описывая квадрат на постоянном расстоянии от прямолинейных участков стенок. За 1 минуту он огибает бассейн 3 раза. Найти расстояние между дельфином и стенкой. Длина каждой стенки 30м.

3. Человек стоит на расстоянии 6 м от реки. На расстоянии 34 м от реки горит костёр. Расстояние между перпендикулярами, опущенными на берег реки из точек, в которых находятся человек и костёр, равно 30 м. Человек бежит со скоростью 5 м/с к реке, зачерпывает ведро воды, потом бежит к костру и заливает его. Какое минимальное время необходимо для этого, если на зачерпывание воды уходит 5 с?

Для записей

Для записей

Цель занятия: Изучить алгоритмы решения ключевых задач на нахождение средней скорости кусочно-равномерного движения и научиться применять их при решении олимпиадных задач по теме.

Существует множество задач на нахождение средней скорости кусочно-равномерного движения, т.е. движения, состоящего из нескольких последовательно проходимых участков, на каждом из которых движение равномерно. Этот тип задач очень часто встречается в физических олимпиадах в 7—9 классах.

Существует две основополагающие, «ключевые» задачи по теме. Назовём их условно: «половина пути» и «половина времени». Рассмотрев эти задачи и получив формулы в общем виде, можно применять их для решения более сложных задач по теме. В этом случае математические преобразования при решении задачи упрощаются. Решение ключевых задач рассмотрено в видеоуроке по теме «Средняя скорость». Ссылка на видеоурок представлена в виде QR кода.

Дадим несколько рекомендаций:

1. При записи условия задачи для его осмысления и анализа используйте схематический рисунок с указанием на нём всех данных задачи.

2. Необходимо сначала решить задачу в общем виде, а затем подставлять числовые значения.

3. Полученные формулы «половины пути» и «половины времени» необходимо запомнить.

4. Нельзя вычислять среднюю скорость как среднее арифметическое скоростей на различных участках пути. (Это справедливо лишь для одного частного случая.)

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

Чтобы считать QR-код необходимо установить на телефон приложение для считывания QR кодов.