Владимир Трошин - Со спичками не шутят

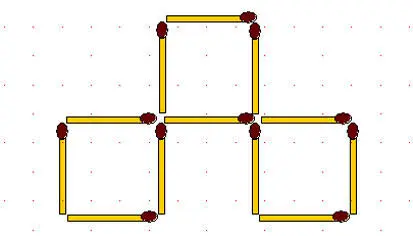
2-38.Переложите эти 12 спичек так, чтобы вдоль каждой стороны четырёхугольника их лежало не четыре, как сейчас, а пять.

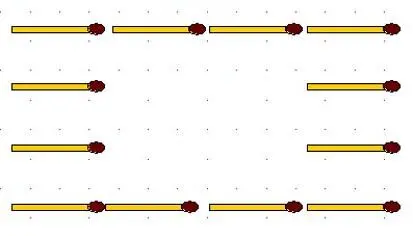
2-39.Изображённые на рисунке 12 спичек требуется переложить так, чтобы вдоль каждой стороны их было:

а) по 5 штук;

б) по 6 штук.

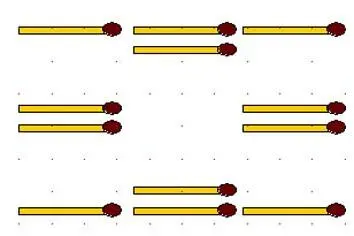
2-40.В фигуре, изображенной на рисунке к задаче 37:

а) переложите 5 спичек так, чтобы получилось всего 2 квадрата;

б) переложите 3 спички так, чтобы получилось 5 квадратов.

2-41.Из спичек сложите правильный шестиугольник и докажите с помощью дополнительного построения и путём рассуждений правильность построения.

2-42.В фигуре, показанной на рисунке:

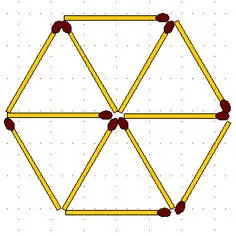
а) переложите 3 спички так, чтобы вместо фигуры из 6 равносторонних треугольников получилась фигура их 6 равных четырёхугольников;

б) переложите 3 спички так, чтобы получилось 7 четырёхугольников, но на этот раз они могут быть не равные.

2-43.В фигуре, изображенной на рисунке:

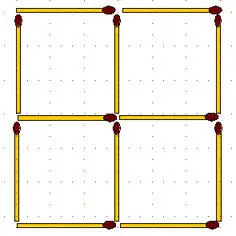
а) переложите 3 спички так, чтобы получилось 3 равных квадрата;

б) переложите 4 спички так, чтобы получилось 3 равных квадрата;

в) переложите 4 спички так, чтобы получилось 2 квадрата;

г) уберите 2 спички так, чтобы осталось 2 квадрата;

д) переложите 2 спички так, чтобы образовалось 7 квадратов (допускается наложение одной спички поперек другой);

е) переложите 4 спички так, чтобы получилось 10 квадратов;

ж) добавьте к исходной фигуре ещё 4 спички так, чтобы квадратов стало 9;

з) расположите те же 12 спичек (все спички должны лежать в плоскости стола) так, чтобы они ограничивали 5 квадратов, причём каждый квадрат должен быть пуст, в противном случае квадраты, изображенные на рисунке, могли бы служить решением, поскольку в качестве пятого мы могли бы считать большой квадрат. Не разрешается ни укладывать две спички одна на другую, ни оставлять свободные концы.

2-44.Спички расположены, как показано на рисунке. Переложите 2 спички так, чтобы получилось 5 равных квадратов.

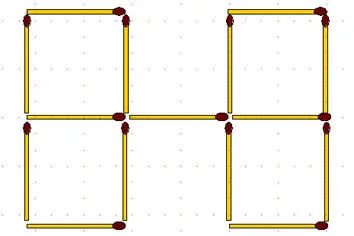
2-45.В фигуре, изображенной на рисунке:

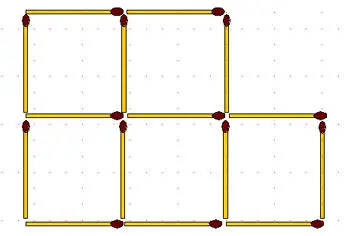
а) снимите 3 спички так, чтобы получилось 3 равных квадрата;

б) переложите 4 спички так, чтобы получилось 3 не равных квадрата;

в) выложите из пяти малых квадратов три, переложив не более 10 спичек.

2-46.Из 16 спичек сложено 5 квадратов. Переложите 2 спички так, чтобы число квадратов уменьшилось на один.

2-47.В пяти квадратах нужно переложить 4 спички так, чтобы получилось 4 квадрата равной величины.

2-48.Передвинув только 2 спички, постройте 4 одинаковых по размеру квадрата.

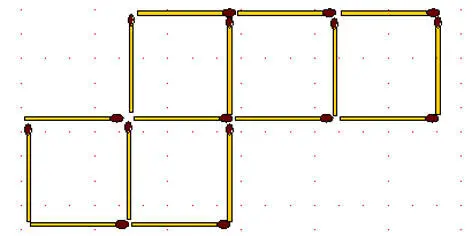
2-49.Уберите как можно меньше спичек так, чтобы оставшиеся спички образовали 4 равносторонних треугольника, таких же размеров, как и 8 треугольников в исходной конфигурации, и нигде не торчали свободные концы.

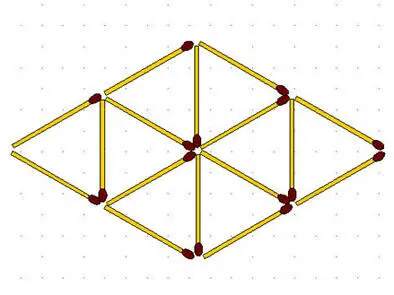
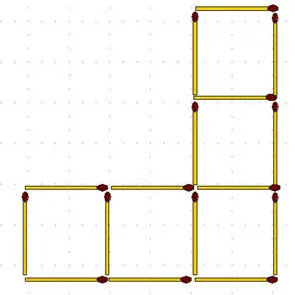
2-50.Уберите 5 спичек так, чтобы осталось только 3 квадрата.

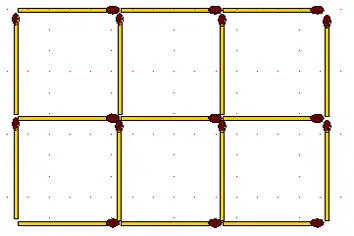
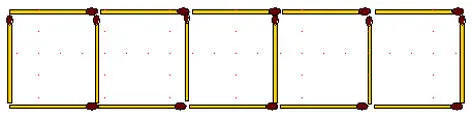
2-51.Уберите 2 спички так, чтобы осталось только 4 квадрата.

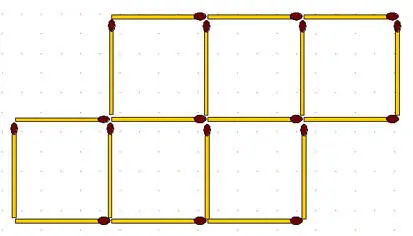
2-52.Из 18 спичек, составляющих 6 равных квадратов, отнимите 2 спички так, чтобы осталось 4 таких же квадрата.

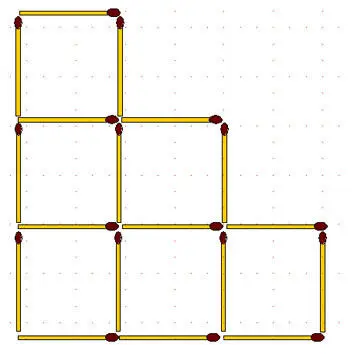
2-53.Из 18 спичек составьте:

а) пять квадратов;

б) один треугольник и 6 четырёхугольников по 3 двух разных размеров.

2-54.Из 18 спичек составьте шесть равных четырёхугольников и один треугольник, в два раза меньший по площади.

2-55.В фигуре, изображенной на рисунке:

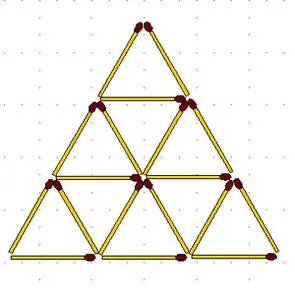
а) убрать 5 спичек так, чтобы осталось 5 треугольников (два решения);

б) переложить 6 спичек так, чтобы получилась фигура, составленная из 6 симметрично расположенных равных четырёхугольников.

2-56.Переложите 7 спичек так, чтобы получилось 4 квадрата.

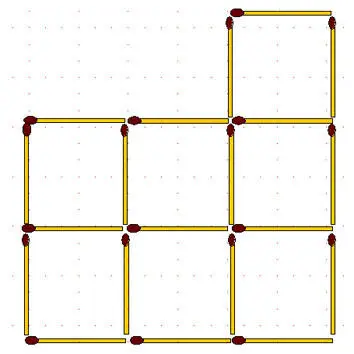
2-57.От 7 квадратов, которые образуют крест и составлены из 22 спичек, отнимите 6 спичек так, чтобы осталось 4 таких же одинаковых квадрата.

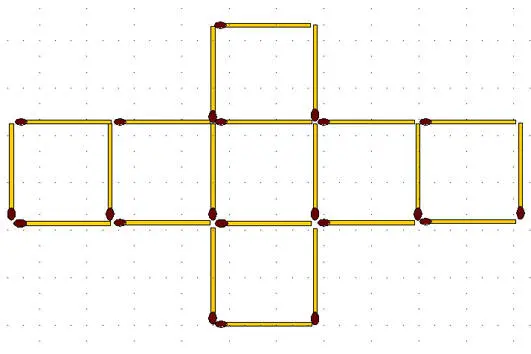
2-58.В изображенной фигуре, переложите 2 спички так, чтобы получилось 7 равных квадратов; затем, из полученной фигуры, уберите 2 спички так, чтобы осталось 5 квадратов.

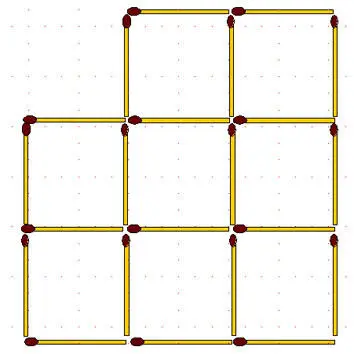
2-59.В фигуре, состоящей из 22 спичек:

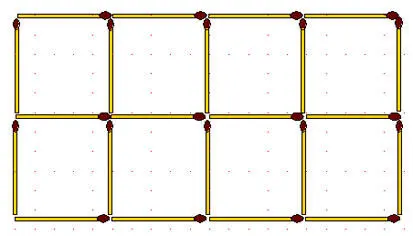
а) убрать 4 спички так, чтобы образовалось 5 равных или 5 неравных квадратов;

б) убрать 6 спичек так, чтобы осталось 4 равных квадрата;

в) убрать 7 спичек так, чтобы осталось 4 равных квадрата.

2-60.Представьте себе, что на рисунке изображен остров, окруженный каналом. Ширина канала как раз равна длине одной спички, так что перебросить мостик через канал с помощью одной спички нельзя: невозможно опереться концами о берег канала. Попробуйте построить мост через канал с помощью 2 спичек, не склеивая и не связывая их концы.