Владимир Трошин - Слова и числа

В русском языке редкостью являются слова, которые не меняются при повороте на 180 0, такие, как местоимение ОНО. В английском языке можно построить целые предложения симметричные относительно поворота на 180 0, например: NOW NO SWIMS ON MON(никто не плавает теперь по понедельникам). Снова небольшое допущение: буквы Wи Mне идеально симметричны, но смысл не нарушают.

Поведем теперь один интересный эксперимент, связанный с зеркальным отражением слов. Напишите на листе прозрачной пленки печатными буквами слово ОТРАЖЕНИЕ. Встав перед настенным зеркалом с этим листком в руках, вы обнаружите неожиданный факт – зеркало не переворачивает это слово! Но в слове ОТРАЖЕНИЕесть буквы, которые при отражении в зеркале непременно должны перевернуться. Почему же они не переворачиваются?

Чтобы понять секрет, нужно немного усложнить приготовления: вырезать буквы слова ОТРАЖЕНИЕиз цветной бумаги, одна сторона которой, например, красная, а обратная сторона белая, и приклеить их на прозрачную пленку.

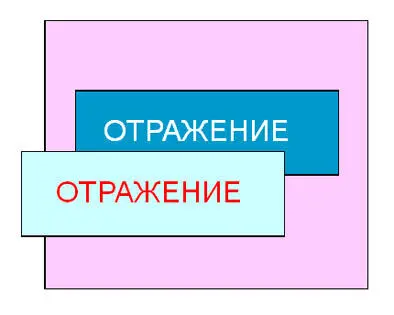
Если теперь вы станете перед зеркалом, повернув пленку красными буквами к себе, то увидите в зеркале это же слово, но составленное из белых букв. Поверните пленку тыльной стороной к себе, и вы увидите перевернутое слово, написанное белыми буквами.

Таким образом, в зеркале отражается слово, составленное из уже перевернутых белых букв тыльной стороны надписи. Получается двойное зеркальное переворачивание надписи, но, как известно из математики, (-1)∙(-1)=+1.

На стеклянных дверях магазинов и других учреждений часто можно встретить надписи вход и выход или от себя и к себе. Если читать эти надписи с обратной стороны стекла, то они превращаются в бессмысленный набор знаков. Договориться бы всем людям и ввести новые слова, например, хот – означающее вход или от себя и тох – означающее выход или к себе, благо эти буквосочетания свободны на данный момент. Тогда одну и ту же надпись, написанную на стекле, можно было бы читать с двух сторон. Проявив тем самым экономию в масштабах отдельно взятой страны и оригинальность мышления.

Эта книга пишется с целью приобщить читателей к творческому поиску, моя задача только дать направление, а далее перед вами неисчерпаемые богатства словарного запаса родного языка. Ищите симметричные слова, составляйте из них осмысленные симметричные предложения. Посмотрите симметрию цифр и чисел [?]Тропинка появится, когда по нетронутому лугу пройдет множество людей в одном направлении.

Аки лев велика

Подробно разработанным вопросом является смысловая симметрия слова, когда оно не переворачивается зеркально, а только читается без изменения справа налево, с конца к началу. Подобные слова и предложения носят название палиндромы, иногда они называются по-русски перевертень, перевертыш. Правда последнее слово мы будем использовать для другого явления в языке, о нем речь пойдет ниже.

Перевертень, палиндром, палиндромон (от греч. palíndromos – бегущий обратно ), слово, фраза или стих, которые могут читаться (по буквам или по словам) спереди назад и сзади наперёд, давая одинаковый смысл. Художественное качество палиндромов зависит от структурных данных языка: в русском и других европейских языках палиндромы обычно звучат искусственно, тогда как, например, на китайском языке в форме палиндрома написано много высокохудожественных стихотворений.

Палиндромы возможны начиная с трехбуквенных слов: боб, дед, кок, мим, око, пуп, шиш. Хотя среди географических названий есть палиндромы из двух букв, например Аа – река в Германии или река Яя в Сибири. Как видите, это понятие менее строгое, чем зеркальная симметрия: слова боб, пуп – палиндромы, но они не симметричны зеркально. Бывший когда-то популярным шведский ансамбль АВВА, чтобы добиться полной симметрии на некоторых своих афишах писал название, переворачивая вторую букву В по вертикали, тогда получалась полная симметрия:

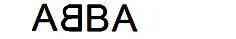
Вот еще несколько примеров пятибуквенных слов-палиндромов: заказ, довод, кабак, казак, комок, наган, потоп, ротор, топот, шабаш, шалаш. Одно из направлений незавершенных поисков в словарных запасах языка – найти как можно более длинное слово палиндром. Например, слово ротатор состоит из семи букв, а есть ли длиннее в русском языке? Есть иноязычные палиндромы, содержащие 11 букв: KINNIKINNIK (разновидность табака, культивируемого индейцами), OOLOOPOOLOO (одно из австралийских наречий), DETARTRATED (выдуманное слово-неологизм, означающее «очищенный от винной кислоты»).

Палиндромы известны во многих языках (например, gig(кабриолет), eve(канун), level(уровень) – в английском), а их история восходит к временам незапамятным. Древнейший из сохранившихся палиндромов написан по-латыни и возник, насколько известно, в IV веке нашей эры. Это фраза «Sator Arepo tenet opera rotas». Перевод, естественно, палиндромом не является: «Сеятель Арепо с трудом держит колеса». Обычно этот палиндром, состоящий из пяти пятибуквенных слов, записывали в клетках квадрата. Необычные свойства этого квадрата заставляли приписывать ему магическую силу, и в этом просматривается параллель с математическими магическими квадратами. И те, и другие квадраты, вырезанные на пластинках из благородных металлов, носили в качестве амулетов, защищающих от болезней и злых духов; их изображения высекались на стенах храмов и дворцов. Ритуальное значение квадратов обуславливалось «дьявольской» сложностью их образования и темнотой малообразованных людей того времени.

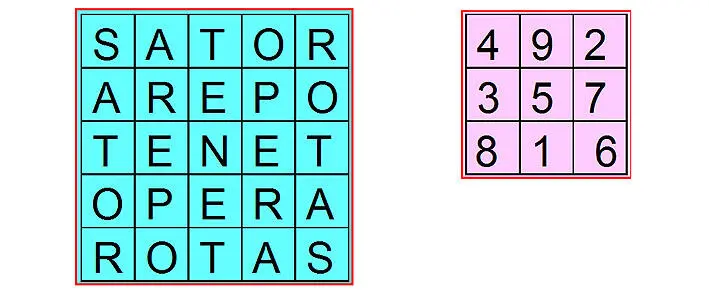
В квадрате с палиндромом его можно прочитать четырьмя способами: по строчкам слева направо и сверху вниз, по строчкам справа налево и снизу вверх, плюс два аналогичных способа по столбцам. Сейчас таким палиндромам, записанным в виде квадратной таблицы и допускающим прочтение четырьмя способами дали название – суперпалиндром . Для квадрата 3×3 известен суперпалиндром Мир или Рим . В математическом магическом квадрате сумма трех чисел по трем строчкам, трем столбцам и двум диагоналям получается одинаковая, равная 15. Как здесь не удивляться, если в хаосе всевозможных размещений букв или цифр, вдруг получается такая гармония. Теперь следите за развитием мысли, мы можем сделать квадрат из букв размером 3×3, а квадрат из цифр размером 5×5.