Владимир Трошин - Слова и числа

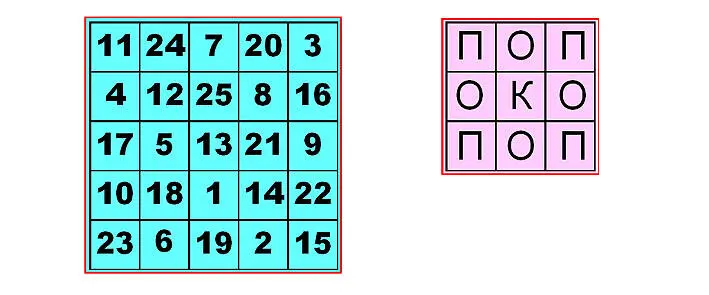
Только теперь магическая сумма математического квадрата равна 65, а палиндромы составлены из слов русского языка. Вот еще одно нераспаханное поле: составить квадраты 4×4, 5×5 с осмысленной фразой-палиндромом на русском языке.

В дальнейшем палиндромы встречались на предметах цилиндрической или сферической формы в виде надписей, которые можно было читать, вращая предмет в любую сторону. От них пошли замкнутые фигуры или «круговертни».

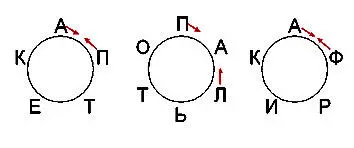
Эти примеры составил математик А.В. Болтрукевич. Если читать их в направлении по стрелке от указанной буквы, то можно прочитать слова аптека и пакет, пальто и лапоть, Африка и факир.

В. В. Маяковский подарил Л. Ю. Брик кольцо, на внутренней стороне которого по кругу были многозначительно выгравированы ее инициалы Л Ю Б, образующие круговертень ЛЮБЛЮ. Маленький, но многозначительный факт истории.

Палиндромами увлекались люди еще до изобретения кроссвордов и сканвордов, считая, что это занятие развивает чувство слова, умение видеть его в глубину, знать его способности выражать множество оттенков смысла и сочетаться с другими словами.

Дети, которые только учатся читать, часто читают вывески магазинов и учреждений наоборот, им интересно, что при этом получается. Потом дети вырастают и перестают заниматься словесной «ерундой», а жаль.

В последнее десятилетие о палиндромах писали журналы «Наука и жизнь» и «Квант», «Загадочная газета» и «Комсомольская правда», печатая много интересных находок своих читателей. Коллективное творчество дает уникальные результаты. Вот несколько примеров предложений палиндромов. В эпиграф вынесен палиндром, который был популярен в нашей стране в начале XIX века, так возвышенно говорили о России. Теперь находят другие темы.

Ленин ел.

Огонь – лоб больного!

Театр тает.

Искать такси.

Да, искать такси – ад.

Осело колесо.

Леша на полке клопа нашел.

На в лоб, болван!

Я не реву – уверен я.

Любители словесных игр не ограничиваются отдельными предложениями, вот пример короткого сочинения о вопросах питания:

Ел еж желе,

А сыр крыса,

Ишак каши,

А жук ужа.

Ужи жижу,

Ил ели.

Я

Мед ем

И щи.

А щи пища.

Автор Алексей Кашеваров

Примеры палиндромов из классики:

«А роза упала на лапу Азора».

А. А. Фет

«Я разуму уму заря.

Я иду с мечем, судия».

Г. Р. Державин

Море могуче. В тон ему, шумен, отвечу Гомером:

Море, веру буди – ярок, скор, я иду буревером.

Д. Авалиани

«Хорошо. Шорох.

Утро во рту.

И клей елки

Течет».

С. Кирсанов – отрывок стихотворения

У Семена Кирсанова несколько палиндромических стихотворений и интересные размышления на эту тему. На русском языке палиндромы писали В. В. Хлебников, В. Я. Брюсов, И. Л. Сельвинский, А. А. Вознесенский.

Через «Sator Arepo» у нас произошел плавный и незаметный переход от отдельный слов палиндромов к палиндромам предложениям. Пошли фразы, в которых каждое отдельное слово не являлось палиндромом, а предложение в целом, если не обращать внимания на расстановку пробелов, палиндромом было. В математике к понятию палиндрома нужен другой подход, потому что, в отличие от слова, любое число, написанное произвольным набором цифр, имеет смысл, например, 1234567890987654321 – вполне реальное число. Только содержательная сторона, изюминка идеи отражения здесь отсутствует, посмотришь на это число, и скажешь: «Ну, и что?». Можно поставить вопрос так: найти квадраты целых чисел, которые неизменно читаются как слева направо, так и наоборот. Некоторые из них найти легко: 11 2=121, 111 2=12321, 1111 2=1234321. Все получившиеся числа палиндромы, и данное правило применимо к любому числу единиц, не превосходящему девяти. Есть и другие случаи, но их найти труднее, например 264 2=69696, 836 2=698896, 2285 2=5221225. Одним вопросом намечено целое направление для поиска числовых палиндромов с определенным смыслом.

Есть палиндромы и среди кубов, например 11 3=1331, причем в большинстве случаев, если куб – палиндром, то и кубический корень из него – тоже палиндром. Далее 11 4=14641. Ожидаемого результата с пятой степенью не получается: 11 5=161051 – не палиндром. Поиск палиндромов среди пятых степеней, пока не дал результатов. Высказана гипотеза, согласно которой не существует чисел палиндромов вида x k при k >4. Её кому-то нужно доказать или опровергнуть [??]

Попробуйте поискать, поэкспериментировать, используя электронную таблицу Excel в офисном пакете. Там есть встроенная функция степени и таблицу чисел легко вводить методом протягивания. Считать не придется, результат определяется только визуально. Если вы владеете любым простейшим языком программирования типа Basic , то можете запрограммировать и вывод итогового палиндрома, если он найдется, конечно. Работа интересная, в мире столько интересного, делал бы сам, но оставляю вам.

Другой вопрос – сколько существует простых чисел палиндромов. Простыми называются числа, не имеющие делителей кроме единицы и самого себя. Среди первых пятидесяти простых чисел я нашел шесть палиндромов: 11, 101, 131, 151, 181, 191. Сколько их всего – неизвестно! Высказывалось предположение о том, что простых чисел палиндромов бесконечно много, но эта гипотеза пока не доказана [??]

Одна знаменитая гипотеза в теории чисел так и называется «гипотеза о палиндромах», и состоит в следующем. Если взять некоторое многозначное число и к нему прибавить число с переставленными в обратном порядке цифрами, потом то же самое проделать с полученной суммой, то, повторяя эти действия несколько раз, вы непременно получите число-палиндром. Гипотеза утверждает, что независимо от того, какое число выбрано, после конечного числа шагов вы непременно получите палиндром.

Иногда для достижения симметричного результата приходится делать большое число шагов, например, для числа 89 ожидаемый результат получается только после 24-го шага. Существует ли число, которое никогда не приведет к симметричному результату? Это никем еще не доказано! Наименьшее число, с которым еще не ясно – это 196. Математики на компьютерах проделали сотни тысяч шагов, но получить палиндром так и не удалось, хотя никем не доказано, что он никогда не появится [??]. Теперь осуществим переход к математическим предложениям палиндромам, есть ведь и такие в богатом мире математики. Для этого нужно использовать математические действия. Начнем со сложения.