Скотт Пейдж - Модельное мышление. Как анализировать сложные явления с помощью математических моделей

Теорема Кондорсе о жюри присяжных

Каждый из нечетного количества людей (моделей) классифицирует неизвестное состояние мира как истинное или ложное. Каждый человек (модель) классифицирует правильно с вероятностью 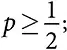вероятность того, что другой человек (модель) выполнит правильную классификацию, статистически независима от правильности классификации любого другого человека (модели).

Теорема Кондорсе о жюри присяжных:большинство голосов обеспечивают правильную классификацию с более высокой вероятностью, чем любой отдельный человек (модель), а по мере увеличения количества членов жюри (моделей) точность решения, принятого большинством, приближается к 100 процентам [38].

Эколог Ричард Левинс объясняет, как применить логику этой теоремы к многомодельному подходу: «Мы пытаемся решить одну и ту же задачу с помощью ряда альтернативных моделей с разными упрощениями, но общим биологическим предположением. В таком случае, если эти модели, несмотря на различие исходных предположений, приводят к аналогичным результатам, мы имеем то, что можно назвать устойчивой теоремой, относительно свободной от деталей модели. Следовательно, истина находится на пересечении независимых случаев лжи» [39]. Обратите внимание, что здесь Левинс рассчитывает на единство классификации. Когда многие модели дают одну и ту же классификацию, наша уверенность должна повыситься.

Следующая теорема, о прогнозе разнообразия, применима к моделям, которые делают численные прогнозы или оценки. Она количественно оценивает влияние точности моделей и их разнообразия на точность их среднего [40] [41].

Теорема о прогнозе разнообразия

Погрешность множества моделей = средняя погрешность модели – разнообразие прогнозов моделей

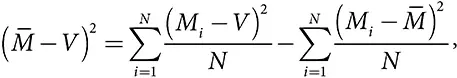
где M i – это прогноз i-й модели, 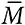– среднее значений моделей, а V – истинное значение.

Теорема о прогнозе разнообразия описывает математическое тождество. Нам не нужно его проверять – оно всегда справедливо. Вот пример. Две модели прогнозируют количество «Оскаров», которые присудят одному из фильмов. Одна модель предсказывает два «Оскара», а другая – восемь. Среднее значение прогнозов двух моделей (прогноз на основе множества моделей) равно пяти. Если на самом деле фильм получит четыре «Оскара», то квадратичная погрешность прогноза первой модели будет равна 4 (2 в квадрате), второй – 16 (4 в квадрате), а множества моделей – 1. Разнообразие прогностических моделей составляет 9, поскольку прогноз каждой модели отличается от среднего прогноза на 3. В таком случае теорему о прогнозе разнообразия можно записать так: 1 (погрешность множества моделей) = 10 (средняя погрешность моделей) – 9 (разнообразие прогностических моделей).

Логика этой теоремы опирается на противоположные (плюсы и минусы) взаимоисключающие типы погрешностей. Если одна модель прогнозирует слишком высокое значение, а другая – слишком низкое, то эти модели демонстрируют разнообразие прогнозов. Обе погрешности исключают друг друга, а среднее значений моделей будет точнее, чем значение каждой модели в отдельности. Даже если оба прогнозируемых значения слишком высоки, ошибка среднего этих прогнозов все равно будет не больше, чем средняя двух завышенных прогнозов.

Из теоремы не следует, что совокупность различных моделей обеспечивает точную картину. Если всем моделям свойственна общая систематическая ошибка, то и среднее тоже будет ее содержать. Данная теорема подразумевает, что любая совокупность различных моделей (или людей) будет точнее, чем средний член этой совокупности – феномен, известный как «мудрость толпы». Этот математический факт объясняет эффективность ансамблевых методов в информатике, которые выводят среднее множества классификаций, а также то, что люди, использующие в рассуждениях множество моделей и концептуальных схем, делают более точные прогнозы по сравнению с теми, кто ориентируется лишь на отдельные модели. Любой однобокий взгляд на мир упускает важные детали и оставляет белые пятна. У таких людей меньше шансов предвидеть крупные события, такие как крах рынка или арабская весна 2011 года [42].

Обе теоремы приводят убедительные аргументы в пользу применения множества моделей, по крайней мере в контексте прогнозирования. Однако порой эти аргументы излишне убедительны. Теорема Кондорсе подразумевает, что при достаточном количестве моделей мы бы практически никогда не ошибались, а теорема о прогнозе – что формирование разнопланового множества умеренно точных моделей прогнозирования позволило бы нам свести погрешность множества моделей практически к нулю. Однако, как мы увидим далее, наша способность строить множество разноплановых моделей не беспредельна.

Чтобы объяснить, почему обе теоремы могут преувеличивать аргументы в пользу многомодельного подхода, прибегнем к моделям категоризации , которые обеспечивают микрообоснования теоремы Кондорсе о жюри присяжных и делят состояния мира на непересекающиеся блоки. Эти модели восходят к эпохе античности. В своем труде The Categories [43]Аристотель выделил десять атрибутов, в том числе такие как субстанция, количество, место и положение, которые использовал для разделения мира на категории. Каждая комбинация этих атрибутов образует отдельную категорию.

Мы используем категории каждый раз, когда употребляем нарицательное существительное. «Брюки» – это категория, так же как «собаки», «ложки», «камины» и «летние каникулы». Нам свойственно использовать категории в качестве руководства к действию. Мы распределяем рестораны по национальному признаку (итальянские, французские, турецкие или корейские), чтобы выбрать, где пообедать. Классифицируем акции по отношению рыночной цены акции к чистой прибыли на одну акцию и продаем малодоходные акции. Используем категории для объяснения тех или иных явлений – как в случае с утверждением, что численность населения Аризоны возросла, потому что в этом штате благоприятные погодные условия. Кроме того, категории применяются для прогнозирования: мы можем предсказать, что у кандидата на государственную должность, имеющего военный опыт, более высокие шансы на победу.

Мы можем интерпретировать вклад моделей категоризации в рамках иерархии мудрости. Объекты образуют данные. Группирование объектов по категориям порождает информацию. Определение оценок по категориям требует знаний. Для критического анализа теоремы Кондорсе мы полагаемся на модель бинарной категоризации , которая делит объекты или состояния мира на две категории – «виновен» и «невиновен». Основная идея состоит в том, что количество соответствующих атрибутов ограничивает число отдельных вариантов категоризации, а значит, и число полезных моделей.