Скотт Пейдж - Модельное мышление. Как анализировать сложные явления с помощью математических моделей

Многие модели работают в теории и на практике. Но это не значит, что многомодельный подход всегда верен. Иногда лучше разработать одну большую модель. В этом разделе мы проанализируем, когда целесообразнее использовать каждый из подходов и попутно рассмотрим вопрос о степени детализации , то есть о том, насколько детальным должно быть разделение данных.

Для того чтобы ответить на первый вопрос (использовать одну большую модель или множество маленьких), вспомните об областях применения моделей: рассуждение, объяснение, разработка, коммуникация, действие, прогнозирование и исследование. Четыре из них (рассуждение, объяснение, коммуникация и исследование) требуют упрощения, благодаря чему мы можем использовать логику, позволяющую объяснять те или иные явления, распространять свои идеи и исследовать возможности.

Вспомните теорему Кондорсе о жюри присяжных. С ее помощью мы смогли раскрыть логику, объяснить, почему подход с использованием множества моделей с большой вероятностью обеспечит правильный результат, и сделать выводы. Если бы мы включили в модель жюри присяжных типы личности и представили доказательства в виде одномерного массива слов, мы заблудились бы в лесу деталей. Борхес рассуждает об этом в своем эссе о науке, рассказывая о составителях карт, стремившихся к чрезмерной детализации: «Коллегия картографов создала карту империи, которая была размером с империю и совпадала с ней до единой точки. Потомки, не столь преданные изучению картографии, сочли эту пространную карту бесполезной» [46].

Модели с высоким уровнем точности будут полезны и для трех оставшихся областей применения моделей, таких как прогнозирование, разработка и действие. При наличии БОЛЬШИХ данных мы должны их использовать. Эмпирическое правило звучит так: чем больше у нас данных, тем детализированнее должна быть модель. Это можно продемонстрировать на примере применения моделей категоризации для структурирования мышления. Допустим, нам нужно построить модель для объяснения вариации во множестве данных. Для создания контекста предположим, что у нас есть огромный массив данных сети продуктовых магазинов, содержащий подробную информацию о ежемесячных расходах нескольких миллионов домохозяйств на продукты питания. По объему расходов они разнятся, что мы измеряем как вариацию – сумму квадратов разности между величиной расходов каждого домохозяйства и средним объемом расходов по всем домохозяйствам. Если средний объем расходов составляет 500 долларов в месяц, а семья тратит 520 долларов, она вносит вклад в общую вариацию, равный 400, или 20 в квадрате [47].

Если общая вариация составляет 1 миллиард долларов, а модель объясняет 800 миллионов этой вариации, то ее показатель R ² составляет 0,8. Величина объясненной вариации соответствует тому, насколько данная модель улучшает оценку среднего значения. Если оценка, полученная с помощью модели, указывает, что домохозяйство потратит 600 долларов, и оно действительно тратит 600 долларов, то данная модель объясняет все 10 000, которые это домохозяйство вносит в общую вариацию. Если семья потратила 800 долларов, а согласно модели должна была потратить 700 долларов, тогда то, что было вкладом в общую вариацию 90 000 ((800 – 500)²), теперь составляет всего 10 000 ((800 – 700)²). Таким образом, данная модель объясняет 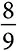вариации.

R² : процент объясненной дисперсии (коэффициент детерминации)

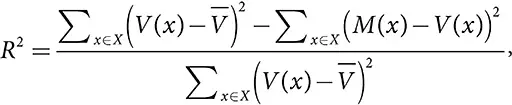
где V(x) – это значение x на множестве X , 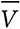– среднее значение, а M(x) – оценка модели.

В данном контексте модель категоризации делит домохозяйства на категории и определяет значение по каждой. Более детализированная модель обеспечивает создание большего числа категорий. Это может потребовать анализа большего количества атрибутов домохозяйств. Увеличение числа категорий позволяет объяснить большую долю вариации, но мы можем зайти слишком далеко. Последовав примеру картографов Борхеса и отнеся каждое домохозяйство к отдельной категории, мы сможем объяснить всю вариацию. Но такое объяснение, как и карта в натуральную величину, не принесет особой пользы.

Создание избыточного количества категорий приводит к чрезмерной подгонке данных, а она препятствует прогнозированию будущих событий. Предположим, мы хотим использовать данные о покупках продуктов за прошлый месяц для прогнозирования данных за нынешний месяц. Ежемесячные расходы домохозяйств отличаются. Модель, которая относит каждое домохозяйство к его собственной категории, предскажет, что оно потратит столько же, сколько и в прошлом месяце. Но это будет не очень хороший прогноз, учитывая ежемесячные колебания расходов. Отнеся домохозяйства к категории им подобных, мы сможем использовать средний объем расходов на продукты аналогичных домохозяйств для создания более точного прогноза.

Для этого мы будем рассматривать ежемесячный объем расходов каждого домохозяйства как одно из значений распределения (о распределениях рассказывается в главе 5). У этого распределения есть среднее значение и дисперсия. Задача построения модели категоризации – создать категории на основе атрибутов таким образом, чтобы у домохозяйств в рамках одной категории были близкие средние значения. Тогда объем расходов одной семьи за первый месяц позволит определить объем расходов другой семьи за второй месяц. Однако ни один вариант категоризации не может быть идеальным. Средний объем расходов домохозяйств, входящих в одну категорию, будет немного отличаться. Мы называем это погрешностью категоризации.

Увеличивая категории, мы увеличиваем и погрешность категоризации, поскольку возрастает вероятность отнесения к одной категории домохозяйств с разными средними значениями. Впрочем, более крупные категории основаны на большем количестве данных, а значит, оценки среднего в каждой категории будут точнее (см. правило квадратного корня в главе 5). Погрешность, возникающая из-за неправильной оценки среднего, называется погрешностью оценки. По мере увеличения категорий погрешность оценки уменьшается. Включение одного или даже десяти домохозяйств в одну категорию не позволит получить точную оценку среднего, если они будут существенно разниться по ежемесячному объему расходов. Тысяча домохозяйств в одной категории обеспечат такую оценку.