Скотт Пейдж - Модельное мышление. Как анализировать сложные явления с помощью математических моделей

См. Arrow, 1963. Общий упорядоченный список альтернатив возможен при ограничении индивидуальных списков предпочтений. Например, если бы у каждого человека был один и тот же список предпочтений, то существовал бы и общий список. В целом у нас нет способа преобразовать индивидуальный список предпочтений в согласованный общий список.

Лучшие умы моего поколения, несомненно, заметили, что я позаимствовал фразу «это действительно было» из поэмы Howl («Вопль»). См. Bickel, Hammel, and O’Connell, 1975.

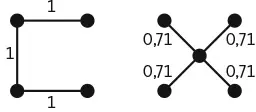
На представленном ниже рисунке показан один из множества примеров того, как включение дополнительной вершины приводит к сокращению общей длины ребер графа. На графе слева четыре вершины соответствуют углам квадрата, а на графе справа добавлена пятая вершина в центре. Если длина стороны квадрата равна 1, общая длина ребер левого графа равна 3, а общая длина ребер правого графа равна 4 × 0,71, что меньше 3.

Парадокс Симпсона возникает, когда заявления на факультеты с более высоким процентом зачисления подает больше абитуриентов женского пола, чем мужского. Например, рассмотрим университет, в котором есть медицинская и ветеринарная школы. Предположим, в медицинскую школу подают заявления 900 абитуриентов мужского пола, и 480 (или 53 процента) из них зачисляются, и 300 абитуриентов женского пола, и 180 (или 60 процентов) из них зачисляются, а в ветеринарную школу подают заявления 100 абитуриентов мужского пола, и 20 (или 20 процентов) из них зачисляются, и 300 абитуриентов женского пола, и 90 (или 30 процентов) зачисляются. В каждой школе на обучение принято больше женщин, но в целом зачислено 50 процентов мужчин (500 из 1000) и только 45 процентов женщин (270 из 600).

В качестве примера парадокса Паррондо рассмотрим следующую ситуацию. Предположим, первая ставка всегда проигрывает 1 доллар, а вторая ставка проигрывает 2 доллара в любом периоде, номер которого не делится на три, и выигрывает 3 доллара в периоды 3, 6, 9, 12 и так далее. Каждая ставка обеспечивает ожидаемый проигрыш, но если вы будете делать вторую ставку только в те периоды, когда она выигрывает, а первую ставку – в остальные периоды, то будете выигрывать по 1 доллару каждые три периода.

См. Kooti, Hodas, and Lerman, 2014.

Предположим, каждый человек получает одинаковый доход I и выплачивает налоги по неизменной ставке налога t. Пусть c обозначает процент сокращения налоговой ставки, а r – повышение уровня дохода. Текущий объем налоговых поступлений в государственный бюджет равен I · t. После снижения налогов объем налоговых поступлений составит I (1 + r ) · t (1 − c ). Объем налоговых поступлений в государственный бюджет увеличится тогда, и только тогда, когда I · t < I (1 + r ) · t (1 − c ). Перегруппировка членов неравенства дает r > c (1 + r ).

См. Ledyard, Porter, and Wessen, 2000, где представлена информация о рыночном механизме, обеспечивающем более эффективное решение многомерных задач полезной нагрузки.

Я позаимствовал слово «непостижимо» у физика Юджина Вигнера (Eugene Wigner, 1960), который описывал математические модели, используемые в естественных науках, как непостижимо эффективные.

См. Ziliak and McCloskey, 2008. В этой книге идет речь о способности моделей, используемых в общественных науках, объяснять вариацию.

Информацию об истории аукциона частот можно найти здесь: Porter and Smith, 2007.

См. Squicciarini and Voigtlander, 2015. В книге Джоэля Мокира (Mokyr, 2002) представлена исчерпывающая историческая информация о важности передачи знаний.

См. www.treasury.gov/initiatives/financial-stability/Pages/default.aspx.

Например, в середине 1990-х годов обанкротились около 60 процентов ресторанов, открывшихся в Колумбусе. Ни один из них не получил финансовой помощи от государства, да и не должен был получить. Здоровая рыночная экономика подразумевает вероятность банкротств. См. Parsa et al., 2005.

Данные взяты из доклада МВФ о глобальной финансовой устойчивости за 2009 год. Сила связи основана на корреляции по стоимости портфеля ценных бумаг. Корреляция рассчитана исходя из предельных случаев – данных за те дни, когда эти учреждения демонстрировали особенно высокие или особенно низкие результаты. Этот показатель должен был отражать вероятность того, что банкротство одной компании повлечет за собой банкротство другой компании. В действительности корреляция по результатам работы могла быть следствием сходства инвестиционных портфелей или того, что один банк владел активами другого банка.

См. Geithner, 2014.

См. Weisberg, 2012. В этой книге описана модель залива Сан-Франциско и ее практическая ценность с точки зрения выбора курса действий.

Исчерпывающую информацию об этом крушении можно найти здесь: Stone et al., 2014.

Я благодарен Джошу Эпштейну за первый пример.

См. Dunne, 1999 и Raby, 2001.

С математической точки зрения эту теорему можно трактовать как получение распределения вероятностей ответов с медианой, центрированной около истинного значения оцениваемой величины. Прим. ред.

См. Levins, 1966.

Более подробное описание теоремы и вывод из нее можно найти здесь: Page 2007, 2017.

Несложно показать, что квадратичная ошибка коллективного предсказания выражается через среднее квадратическое расстояние отдельных прогнозов от коллективного прогноза. Прим. ред.

Мудрость толпы – тема одноименной книги Джеймса Шуровьески (Suroweicki, 2006); о том, как лисы могут перехитрить ежей, можно прочитать в книге Филипа Тетлока (Tetlock, 2005); в статье Статиса Каливаса (Kalyvas, 1999) идет речь о неспособности политической науки предвидеть падение Советского Союза; информацию об использовании ансамблевых методов в области компьютерных наук можно найти здесь: Patel et al., 2011.

См. Аристотель. Сочинения в 4 томах. Том 2. М.: Мысль, 1978. Прим. ред.

Лу Хонг и Скотт Пейдж показывают в своей статье (Hong and Page, 2009), что независимые модели требуют уникального набора категорий. Другими словами, существует только один способ создания множества независимых прогнозов на основе модели бинарной категоризации.

См. три мои книги, опубликованные ранее: «Различие» (The Difference – Page, 2008), «Разнообразие и сложность» (Diversity and Complexity – Page, 2010) и «Преимущества разнообразия» (The Diversity Bonus – Page, 2017) – в них подробно анализируется теорема о прогнозе разнообразия. Данные об экономических прогнозах можно найти здесь: Mannes, Soil, and Larrick, 2014.