Скотт Пейдж - Модельное мышление. Как анализировать сложные явления с помощью математических моделей

В научной литературе описаны десятки вариантов применения моделей. Мы же остановимся на семи: рассуждение, объяснение, прогнозирование, разработка, коммуникация, действие и исследование.

Области применения моделей (REDCAPE)

Рассуждение:определение условий и вывод логических следствий.

Объяснение:предоставление (поддающихся проверке) объяснений эмпирических явлений.

Разработка:выбор характеристик институтов, политик и правил.

Коммуникация:передача знаний и представлений.

Действие:обеспечение выбора политических альтернатив и стратегических действий.

Прогнозирование:получение численных и категорийных прогнозов будущих и неизвестных явлений.

Исследование:изучение возможностей и гипотез.

При построении модели мы выделяем такие важные составляющие, как агенты и объекты, наряду с соответствующими характеристиками, а затем описываем способы взаимодействия и объединения отдельных фрагментов, что позволяет определить, что из чего следует и почему. Такой подход повышает эффективность наших рассуждений. Хотя полученные выводы зависят от исходных предположений, процесс рассуждений раскрывает нечто большее, чем тавтологии. Крайне редко можно получить весь спектр последствий наших предположений только из одного наблюдения – нужна еще и формальная логика. Логика позволяет раскрыть возможности и невозможности. С ее помощью можно установить точные и порой неожиданные связи. Это позволяет обнаружить обусловленность интуитивных выводов.

Теорема Эрроу (теорема невозможности) – пример того, как логика раскрывает невозможное. Модель рассматривает вопрос о том, приводит ли объединение индивидуальных предпочтений к формированию коллективного предпочтения. Предпочтения представлены в ней в виде упорядоченного списка альтернатив. Применительно к пяти итальянским ресторанам, обозначенным буквами от A до E, эта модель допускает любой из 120 упорядоченных списков. Согласно введенным Эрроу требованиям, общий упорядоченный список должен быть монотонным (если каждый ставит в своем списке A выше B, то же происходит в общем списке), независимым от посторонних альтернатив (если относительный ранг A и B в каждом списке остается неизменным, а ранг других альтернатив меняется, то порядок A и B в общем упорядоченном списке не меняется) и недиктаторским (ни один человек не должен определять общий упорядоченный список альтернатив). Далее Эрроу доказывает, что если разрешены любые предпочтения, то коллективное упорядочение списка может и не существовать [21].

Кроме того, логика раскрывает парадоксы. Применение моделей позволяет продемонстрировать возможность ситуации, когда в каждой подгруппе содержится более высокий процент женщин, чем мужчин, но в общей совокупности наблюдается более высокий процент мужчин. Этот феномен известен как парадокс Симпсона. И он действительно имел место: в 1973 году Калифорнийский университет в Беркли зачислил на большинство факультетов больше студенток, чем студентов. Однако в целом университет принял больше студентов мужского пола. Модели также показывают, что чередование двух проигрышных ставок может обеспечить положительный ожидаемый результат (Парадокс Паррондо); или что включение дополнительной вершины в граф позволяет сократить общую длину ребер, необходимых для соединения всех вершин [22].

Не следует отбрасывать эти примеры как математические новшества. Каждый из них имеет практическое применение: усилия по увеличению численности женщин могут иметь обратный эффект, сочетание проигрышных инвестиций способно обеспечить выигрыш, а общую длину сети электрических линий, трубопроводов, Ethernet-линий или дорог можно сократить путем добавления дополнительных узлов.

Логика также раскрывает математические зависимости. Исходя из аксиом Эвклида, треугольник однозначно определяется любыми двумя углами и стороной или любыми двумя сторонами и углом. Стандартные предположения о поведении потребителей и компаний позволяют сделать вывод, что на рынках с большим количеством конкурентов цена равна предельным издержкам. Некоторые результаты оказываются неожиданными, как в случае парадокса дружбы , который гласит, что в любой сети дружеских связей у друзей человека больше друзей, чем у него самого.

Этот парадокс объясняется тем, что у очень популярных людей больше друзей. На рис. 2.1 показана сеть дружеских связей в клубе карате, описанная Уэйном Закари. У человека, представленного черным кружком, шесть друзей, которые обозначены серыми кружками. У его друзей в среднем семь друзей, отмеченных белыми кружками. В целом в сети двадцать девять из тридцати четырех человек имеют друзей, которые пользуются большей популярностью, чем они сами [23]. Далее вы увидите, что если сделать ряд других допущений, то друзья большинства людей в среднем будут также более красивыми, добрыми, богатыми и умными, чем они сами.

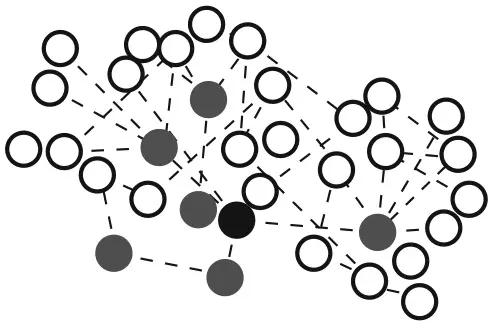
Рис. 2.1.Парадокс дружбы: у друзей человека больше друзей, чем у него самого

И последнее, самое важное: логика раскрывает обусловленность истины. Политик может утверждать, что снижение налогов увеличивает налоговые поступления в государственный бюджет, стимулируя экономический рост. Простейшая модель, в которой доход исчисляется как произведение налоговой ставки на уровень дохода, доказывает, что объем налоговых поступлений увеличивается только в случае, если процентный рост дохода превышает процентное сокращение налогов [24]. Следовательно, 10-процентное снижение подоходного налога увеличит объем налоговых поступлений только тогда, когда приведет к повышению уровня доходов более чем на 10 процентов. Логические рассуждения политика верны лишь при некоторых условиях, которые позволяют определить модели.

Сила обусловленности становится очевидной при сопоставлении утверждений, полученных с помощью моделей, и описательных утверждений, пусть и имеющих эмпирическое обоснование. Рассмотрим управленческую поговорку «в первую очередь самое важное» , смысл которой сводится к тому, что при наличии множества задач прежде всего нужно решать самую важную. Это правило также известно как «сначала крупные камни» , поскольку, складывая в ведро камни разных размеров, сначала вы должны уложить большие камни, потому что если первыми сложить мелкие камни, то крупные могут не поместиться.