Каниа Кан - Нейронные сети. Эволюция

Что если сделать так, что на числовых координатах, все данные которые будут находится выше линейной функции, будут принадлежать к одному классу, а ниже к другому. То есть функция прямой будет служить нам как классификатор.

Давайте покажем вышесказанное на слайде:

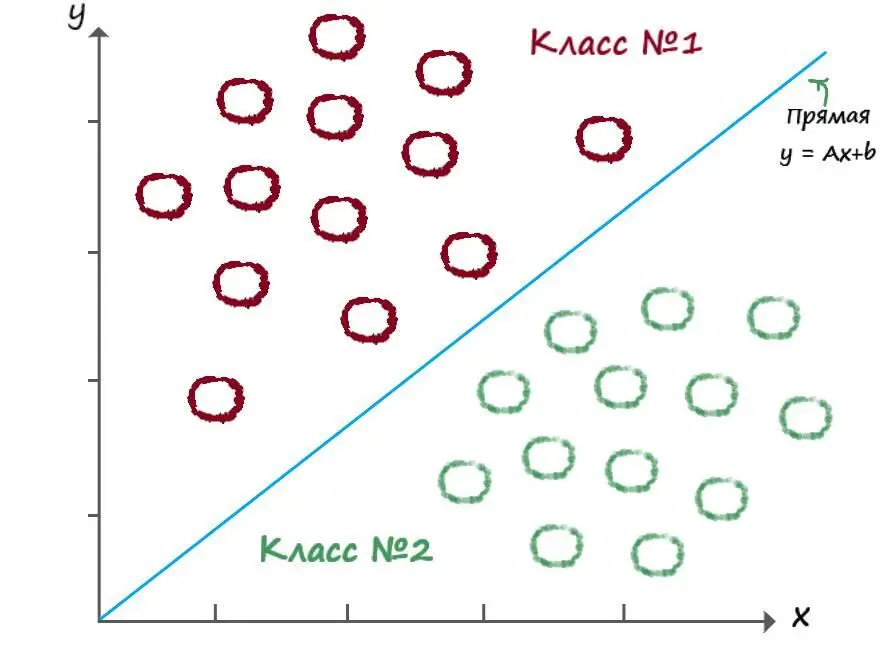
Отлично! Теперь осталось вспомнить что представляет из себя линейная функция.

Вспоминая школьный курс математики, из которого нам должно быть известно, что коэффициент А, в уравнении прямой, отвечает за её наклон. Чем больше значение коэффициента А, тем больше крутизна наклона линии. А коэффициент b– отвечает за точку начала координат по оси Y, через которую проходит прямая.

Раз мы еще толком не знаем, как будем действовать, давайте максимально всё упрощать. Будем считать, что прямая проходит через начало координат и соответственно параметр прямой b, обратим в ноль: b = 0. Тогда окончательное выражение нашей разделительной линии, станет еще более простым:

y = Ax

Пусть нашим заданием будет – классифицировать два вида животных, определенной возрастной группы, в два дня от роду, по размеру их тела – высоте и длине.

Для начала, подберем всего две выборки, которые разительно отличаются друг от друга:

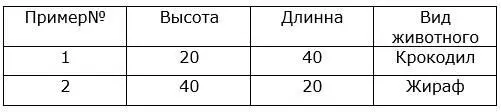
Примем за х– значение длины, а за y– значения высоты. Визуализируем эти данные на числовой прямой:

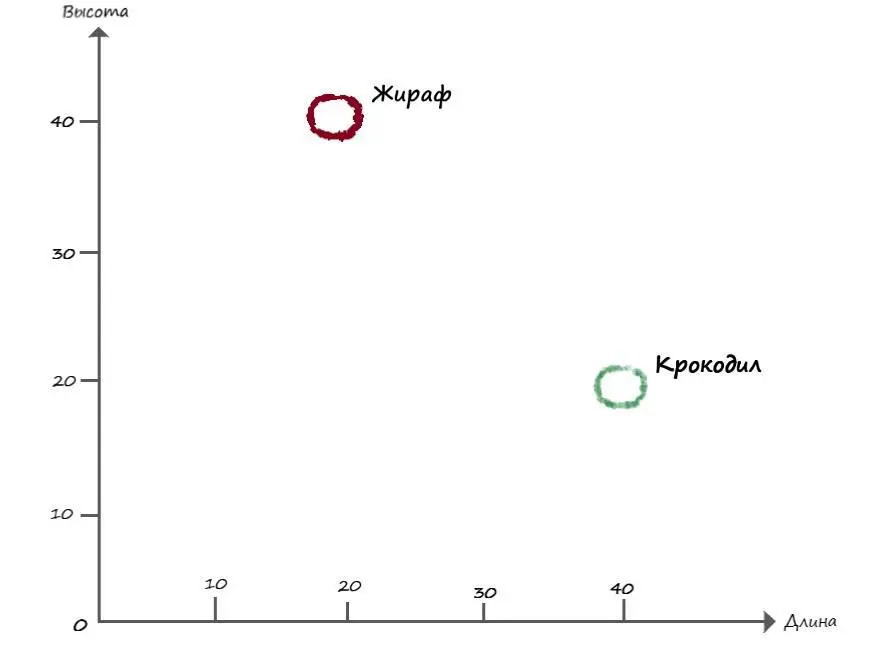
Нужно придумать как разделить эти два вида линейной функцией. Попробуем мыслить последовательно.

Для начала, попробуем разделить наши данные случайной разделительной линией. Для этого примем значение коэффициента крутизны любым случайным числом, пусть А = 0,4. Тогда наше уравнение разделительной линии примет вид – y = 0,4x.

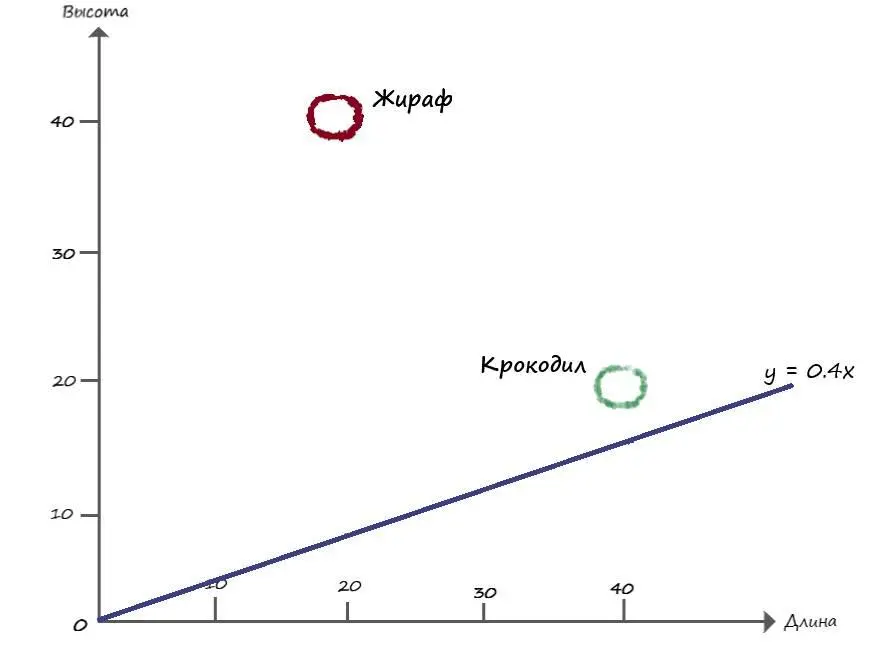
Как следует из графика, линия – y = 0,4 x, не отделяет один вид от другого. Для выполнения условия, её необходимо поднять выше. Для этого нам потребуется выработать последовательность команд и математические правила. Говоря иными словами, проработать алгоритм, когда при подаче данных из нашей таблицы (длины и ширины видов животных), в конечном итоге разделительная линия будет четко разделять эти два вида.

Теперь давайте протестируем нашу функцию на первом тренировочном примере, соответствующему виду крокодила, где: высота крокодила – 20, длина – 40. Не важно в чем будем измерять, в какой метрической системе. Самое близкое по условию это сантиметры. Но будем считать, что измеряем в условных единицах. Возьмём пример, где х=40(длинна=40), и подставив в него значение нашего коэффициента А = 0,4, получим следующий результат:

y = Ax = (0,4) * (40) =16

На выходе получили значение высоты y = 16, а верный ответ y =20.

Для того чтоб исправить положение и приподнять нашу линию, введем понятие ошибки Е, с помощью следующей формулы:

Е = целевое значение из таблицы – фактический результат

Следуя этой формуле:

Е = 20 – 16 = 4

Теперь давайте приподнимем нашу линию на 4 пункта выше и отобразим это на графике:

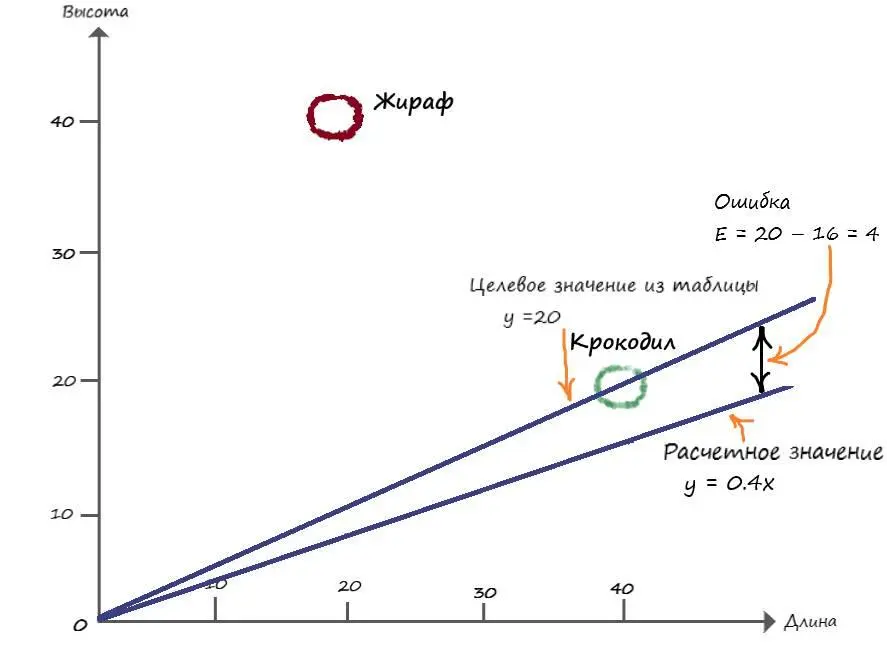
Ну и тут, как мы можем наблюдать, наша линия проходит через точку определяющую вид – крокодил, а нам надо чтобы линия лежала выше.

Решается эта проблема очень легко, давайте примем наши целевые значение чуть больше, положим высоту у = 21, вместо у = 20. И снова пересчитаем ошибку с новыми параметрами:

Е = 21 – 16 = 5

Отобразим новый результат на координатах:

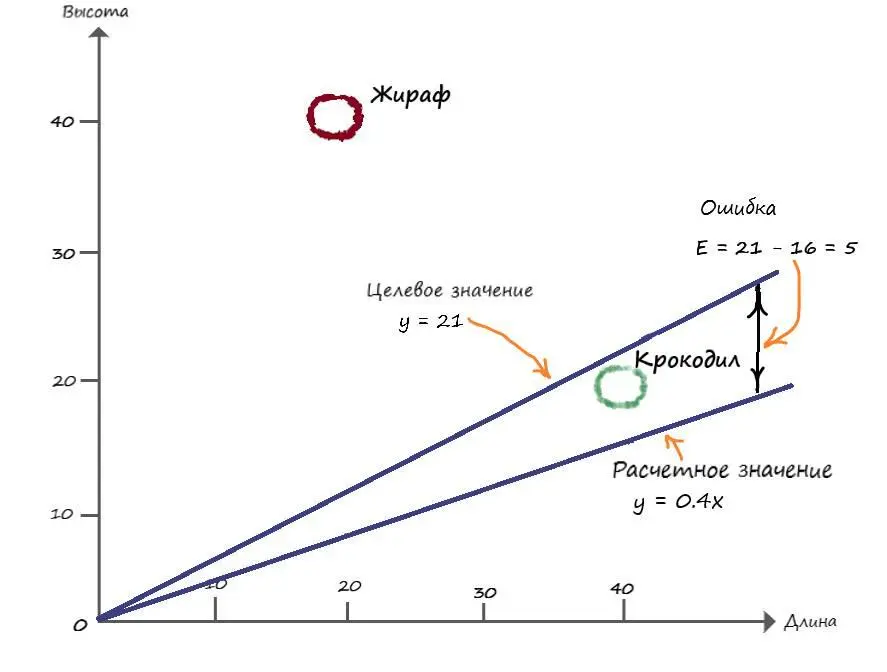
В итоге имеем новую прямую с новым значением коэффициента крутизны. Найдя этот коэффициент, мы как раз и сможем построить нужную нам прямую, на всех значениях оси x (длины).

Для этого нам необходимо через наше значение ошибки Е, найти искомое изменения коэффициента А. Чтоб это сделать, нам нужно знать, как эти две величины связаны между собой, тогда мы бы знали, как изменение одной величины влияет на другую.

Начнем с линейной функции:

y = Ax

Обозначим переменной T– целевое значение (наше значение из таблицы). Если ввести в искомый коэффициент А, такую поправку как: А+∆А = искомое А.

Тогда целевое значение можно определить, как:

T = (А + ∆ А) х

Отобразим последнее соотношение на графике:

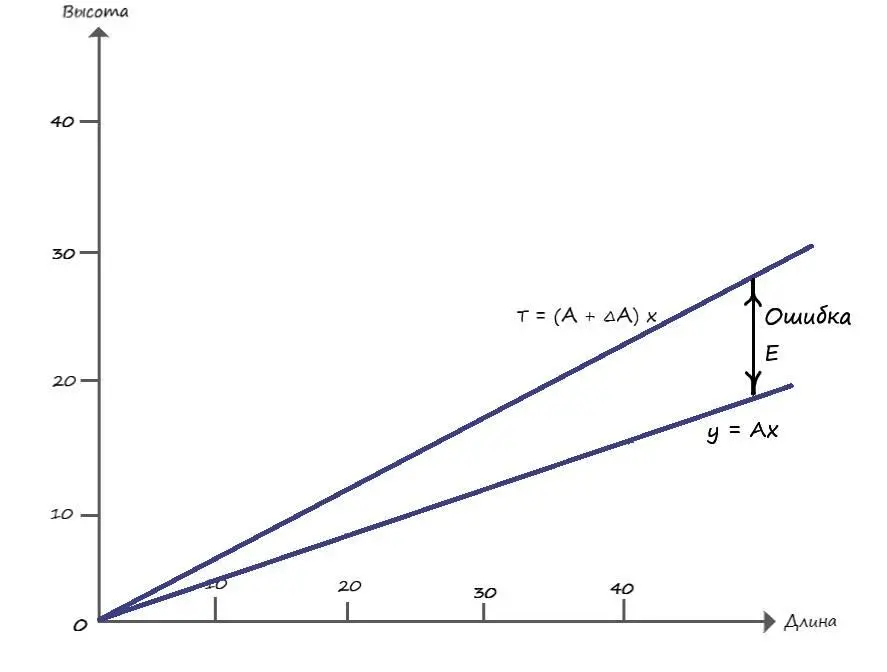
Подставим эти значения в формулу ошибки Е = T – у:

Е = T – у = (А + ∆А) х – Ах = Ax + (∆А) х – Ах = (∆А)х

Е = (∆А)х

Теперь зная, как ошибка Есвязана с ∆А, нетрудно выяснить что:

∆А = Е / х

Отлично! Теперь мы можем использовать ошибку Едля изменения наклона классифицирующей линии на величину ∆Ав нужную сторону.

Давайте сделаем это! При x = 40и коэффициенте А = 0,4, ошибка E = 5, попробуем найти величину ∆А:

∆А = Е/х = 5 / 40 = 0,125

Обновим наше начальное значение А:

А = А+ ∆А = 0,4 +0,125 = 0,525

Получается новое, улучшенное, значение коэффициента А = 0,525. Можно проверить это утверждение, найдя расчетное значение ус новыми параметрами:

y = А х = 0,525 * 40 = 21

В точку!

Теперь давайте узнаем на сколько надо изменить коэффициент А, чтоб найти верный ответ, для второй выборки из таблицы видов – жираф.

Целевые значения жирафа – высота y = 40, длина x = 20. Для того чтобы, разделительная линия не проходила через точку с параметрами жирафа, нам необходимо уменьшить целевое значение на единицу – y = 39.

Подставляем x = 20в линейную функцию, в которой теперь используется обновленное значение А=0,525:

у = Ax = 0,525 * 20 = 10,5