Каниа Кан - Нейронные сети. Эволюция

Добавив на второй вход параметр ( b), отвечающий за точку прохождения прямой через ось Y, в качестве обучаемого коэффициента, мы получаем весь арсенал возможностей линейной функции ( y = Ax + b) при классификации.

Так как у параметра ( b), в линейной функции ( y = Ax 1+ b), нет произведения на значение переменной, то на второй вход, в качестве данных, всегда поступает единица ( x 2 = 1). Откуда на выходе получаем взвешенную сумму: y = Ax 1+ bx 2. При х2 = 1, на выходе получаем y = Ax 1+ b. И наконец, назвав коэффициенты, при входных данных – весовыми коэффициентами, изменили их обозначение – w 1 = А, а w 2 = b, в итоге: y = w 1 x 1+ w 2.

Но обучая наш нейрон, как в первом случае, на выходе мы не получим нужных ответов. Оказалось, всё дело в том, что второй вход, участвует в процессе обучения независимо от первого, и наоборот. Каждый тянет одеяло на себя. Оба входа, как бы мешают друг другу подстроить свои веса. Вследствие чего, при вычислении ошибки, получали непредсказуемый результат для подстройки обоих весовых коэффициентов. И было бы здорово, если бы с каждым последующим обучающим примером, мы смогли уменьшать функцию ошибки.

Для решения этой проблемы, нам пришлось ознакомится с методом градиентного спуска. В ходе рассмотрения этого метода, мы ознакомились с производными, узнали о правилах дифференцирования. В следствии чего, научились обновлять весовые коэффициенты, в сторону уменьшения ошибки по каждому из входов.

Суть метода – обновление весовых коэффициентов на своих входах, в зависимости от функции ошибки, таким образом, чтобы плавно двигаться в сторону её уменьшения. Другими словами, найти на каждом из входов, такое значение веса, чтоб ошибка на выходе, для всех этих весовых коэффициентов, была минимальной и как следствие удовлетворяла их всех.

Получив необходимые выражения, убедились, что изменений в математике функционирования искусственного нейрона, не так уж и много. Подобно биологической эволюции, наша тоже произошла постепенно. Ранее приобретённые навыки для классификации, лишь немногим усовершенствовались, а новые в свою очередь, выходят исходя из старых.

А что будет если добавить на вход искусственного нейрона, еще больше данных? Для начала, хотя бы еще один…

Допустим поступило новое задание, не совсем похожее на предыдущее. Теперь от нас хотят классифицировать виды животных, но уже с дополнительным параметром – возраст. Тестовая выборка дается уже по трем параметрам – ширина, высота, возраст. Первое что приходит в голову – объединить два параметра в одно. Если принять соотношение длины к высоте за один параметр, то мы можем смело действовать, как раньше:

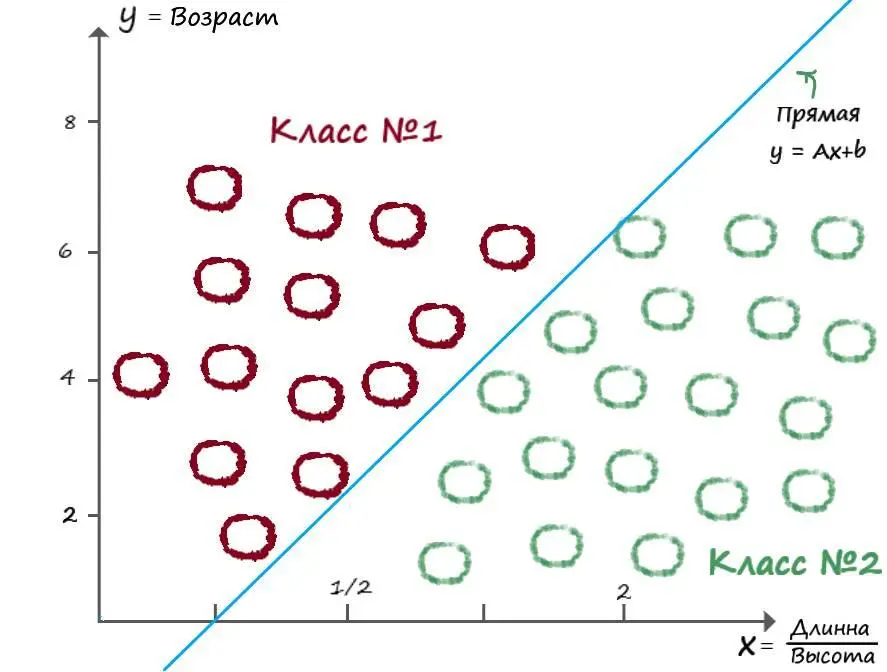
Но проанализировав всё задание самостоятельно, мы пришли к такому выводу:

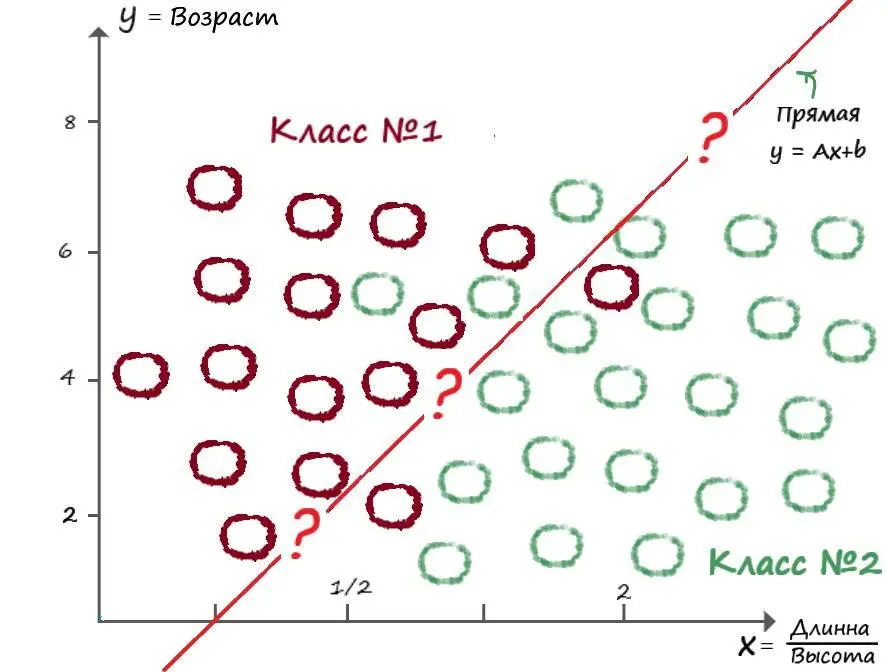
Как видим – данные пересекаются. И действительно, природу, как и всё что нас окружает, далеко не всегда можно классифицировать прямой. Даже один и тот же вид животных, может обитать в разных климатических зонах и условиях, что может сильно сказываться на параметрах его тела.

Что же делать? Ну для начала не будем паниковать и попробуем найти решение, пойдя по простому пути.

Рассмотрим, что будет на выходе нашего нейрона, добавив к нему еще один вход. Для этого, будем подавать на его вход данные логических функций.

Логическая функция принимает на вход два аргумента. Их значения, целевые значения, тоже известны. Логические функции могут принимать только дискретные аргументы (0 или 1).

Рассмотрим логическую функцию (И). Такая функция равна нулю для любого набора входных аргументов, кроме набора (х1 = 1, х2 = 1):

Функцию логического (И), для упрощения, еще называют – логическом произведением. В самом деле:

х1 * х2 = 0 * 0 = 0

х1 * х2 = 1 * 0 = 0

х1 * х2 = 0 * 1 = 0

х1 * х2 = 1 * 1 = 1

Раз мы решили добавить еще один вход на наш нейрон, то как будет выглядеть функция выхода? Ну первое что приходит в голову, раз мы в первом случае суммировали, по аналогии с линейной функцией, два произведения входных данных и весовых коэффициентов ( y = w 1 x 1 + w 2), то почему бы не попробовать действовать подобным образом. Тогда представим линейный классификатор функцией – y = w 1 x 1 + w 2 x 2 + w 3. Ну и конечно же, эволюционируем наш нейрон, добавив еще одну “ногу” на вход:

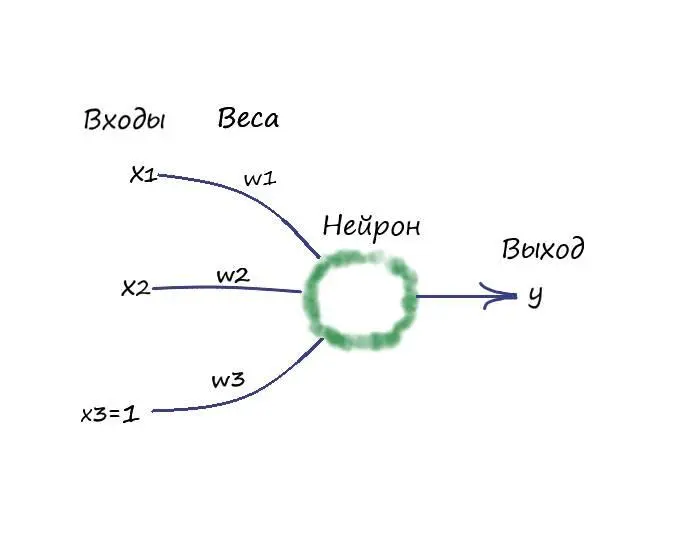
Если присмотреться, наш нейрон уже и в правду напоминает какой то, простейший живой организм.

Так как у нас всего четыре обучающие выборки, то давайте самостоятельно, без написания программы, проанализируем, что будет происходить на выходе и какие должны быть значение весовых коэффициентов:

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.