Каниа Кан - Нейронные сети. Эволюция

Решим найденным способом, наш первый пример, когда скорость автомобиля была постоянной, на всем промежутке времени. В этом примере, приращение функции равно нулю ( ∆ s = 0), и соответственно тангенса угла не существует:

∆s = s(t+∆t) – s(t) = s(t) – s(t) = 0

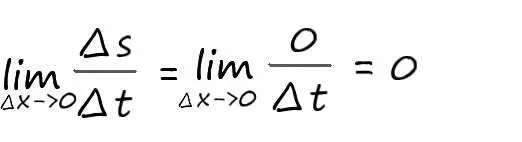
Итак, имеем первый результат – производная константы равна нулю. Этот результат мы уже выводили ранее:

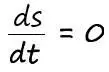
Откуда можно сформулировать правило, что производная константы, равна нулю.

s ( t ) = с, где с – константа

с′ = 0

Запись с′– означает что берется производная по функции.

Во второй примере, когда изменение скорости автомобиля проходило линейно, с постоянным изменением, найти производную функции ( s = 0,2 t + 1,5), не зная правил дифференцирования сложных функций, мы пока не сможем, поэтому отложим этот пример на потом.

Продолжим с решения третьего примера, когда изменение скорости автомобиля проходило не линейно:

s = t ²

Приращение функции и производная:

s(t) = t²

∆s = s(t+∆t) – s(t) = (t+∆t) ² – t² = t² + 2t∆t + ∆t² – t² = ∆t(2t+∆t)

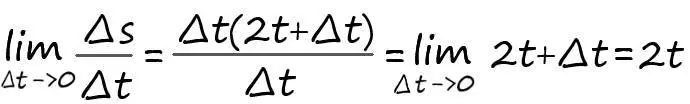
Вот мы и решили наш третий пример! Нашли формулу точного изменения скорость от времени. Вычислим производную, в всё той же точки t = 3.

s ( t ) = t ²

s ′( t ) = 2*3 = 6

Точный ответ, в пределах небольшой погрешности, почти сошелся с вычисленном до этого приближенным ответом.

Попробуем усложнить пример. Предположим, что скорость движения автомобиля описывается кубической функцией времени:

s ( t ) = t ³

Приращение и производная:

s(t) = t³

∆s = s(t+∆t) – s(t) = t³ + 3 t²∆t+ 3t∆ t² + ∆ t³ – t³ = ∆t(3 t² + 3t∆t + ∆t²)

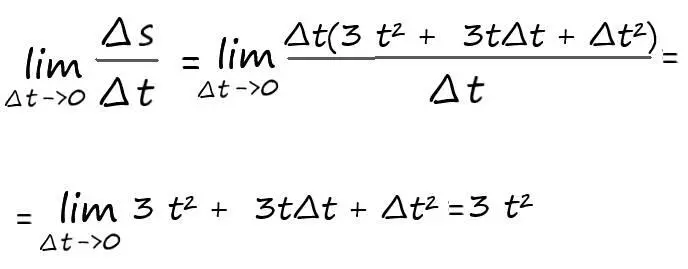
Из двух последних примеров (с производными функций s ( t ) = t ²и s ( t ) = t ³) следует, что показатель степени числа, становится его произведением, а степень уменьшается на единицу:

s ( t ) = tⁿ

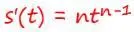
А чему равна производная от аргумента функции? Давайте узнаем…

s ( t ) = t

Приращение:

∆ s = s ( t +∆ t ) – s ( t ) = t + ∆ t – t = ∆ t

Производная:

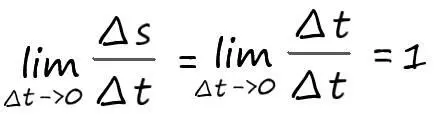
Получается, что производная от переменной:

t ′ = 0

Дифференцирование суммы

( u + v )′ = u ′ + v ′, где uи v– функции.

Пусть f(x) = u(x) + v(x). Тогда:

∆ f = f ( x +∆ x ) – f ( x ) = u ( x +∆ x ) + v ( x +∆ x ) – u ( x ) – v ( x ) = u ( x ) + ∆ u + v ( x ) + ∆ v – u ( x ) – v ( x ) = ∆ u + ∆ v

Тогда имеем:

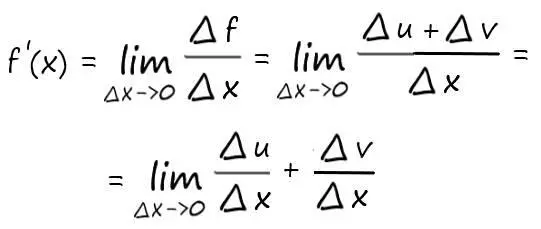
Дроби ∆ u /∆хи ∆ v /∆хпри ∆х->0стремятся соответственно к u ′( x )и v ′ ( x ). Сумма этих дробей стремится к сумме u ′( x ) + v ′ ( x ).

f ′( x ) = u ′ ( x ) + v ′ ( x )

Дифференцирование произведения

( u * v )′ = u ′ v + v ′ u, где uи v– функции

Разберем, почему это так. Обозначим f ( x ) = u ( x ) * v ( x ). Тогда:

∆ f = f ( x +∆ x ) – f ( x ) = u ( x +∆ x ) * v ( x +∆ x ) – u ( x ) * v ( x ) = ( u ( x ) + ∆ u ) * ( v ( x ) + ∆ v ) – u ( x ) * v ( x ) = u ( x ) v ( x ) + v ( x )∆ u + u ( x )∆ v + ∆ u ∆ v – u ( x ) v ( x ) = v ( x )∆ u + u ( x )∆ v + ∆ u ∆ v

Далее имеем:

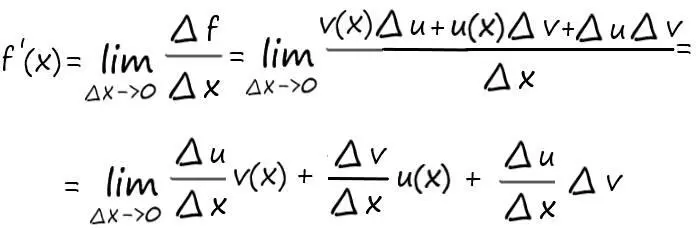
Первое слагаемое стремиться к u′(x) v(x). Второе слагаемое стремиться к v′(x)* u(x). А третье, в дроби ∆ u /∆ x, в пределе даст число u′(x), а поскольку множитель ∆vстремиться к нулю, то и вся эта дробь обратится в ноль. А следовательно, в результате получаем: