Каниа Кан - Нейронные сети. Эволюция

Напомню, дифференциальное исчисление сводится к нахождению изменения одной величины в результате изменения другой. В данном случае нас интересует, как скорость изменяется со временем.

Сказанное, можно записать в следующей математической форме:

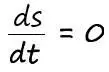
Линейное изменение

А теперь представим тот же автомобиль, с начальной скоростью 1,5 км/мин, но в определенный момент, водитель жмет на газ, и автомобиль начинает набирать скорость (равномерно ускоряться). И по истечении трех минут, от момента, когда мы нажали педаль газа, его скорость станет равной 2,1 км/мин.

Из графика видно, что увеличение скорости автомобиля, происходит с постоянной скоростью изменения (равномерным ускорением), откуда функция зависимости скорости от времени, выглядит как прямая линия.

Изначально, в нулевой момент времени, скорость равна 1,5 км/мин. Далее мы добавляем по 0,2 км в минуту. Таким образом, искомое выражение приобретает следующий вид:

Скорость = 1,5 + (0,2 * время)

S = 1,5 + 0,2 t

В итоговом выражении, вы легко увидите уравнение прямой. Где коэффициент = 0,2 – величина крутизны наклона прямой, а постоянный член = 1,5 – точка через которую проходит линия на оси координат y.

Так будет выглядеть выражение, которое скажет нам о том, что между скоростью движения автомобиля и временем существует зависимость:

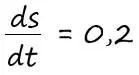
Каждую минуту, скорость изменяется на значение 0,2.

Не равномерное изменение

Возьмём всё тот же автомобиль, который стоит на месте. Сидя в нем, вы начинаете жать в “пол” педаль газа, удерживая её в этом положении. Скорость движения автомобиля, за счет инерции, будет возрастать не равномерно. Ежеминутное приращение скорости будет с каждой минутой увеличиваться.

Приведем в таблице, значения скорости в каждую минуту:

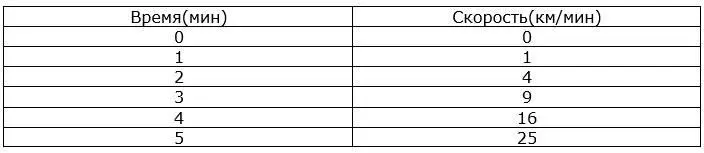
Эти данные представляют собой выражение:

s = t ²

Какова скорость изменения скорости автомобиля в каждый момент времени?

Если посмотреть на два предыдущих примера, то в них скорость изменения скорости определялась наклоном графика, коэффициентом крутизны прямой линии А. Когда автомобиль двигался с постоянной скоростью, его скорость не изменялась, и скорость изменения скорости равна 0. Когда автомобиль равномерно набирал скорость, скорость его изменения составляла 0,2 км/мин, на протяжении всего времени движения автомобиля в этом режиме.

А как тогда поступить в этом случае? Как узнать изменение скорости по кривой?

После трех минут с момента начала движения (t=3), скорость составит 9 км/мин. Сравним со скоростью в конце пятой минуты. После пяти минут с момента начала движения (t=5), скорость составляет 25 км/мин. Не важно, что скорость 25 км/мин – сопоставима со скоростью пули, ведь это воображаемая машина, и едет она с той скоростью, с какой мы захотим. Если провести касательную линию в этих точках, то окажется, что угол наклона у них совершенно разный:

Вы видите, что чем больше скорость в точке касательной, тем её наклон круче. Оба наклона представляют искомую скорость изменения скорости движения. Можно сравнить с вторым примером – линейное изменение.

Но как измерить наклон этих линий? Для этого давайте представим, что наша касательная (t = 3, s = 9), пересекает функцию в двух точках, расстояние между которыми очень мало:

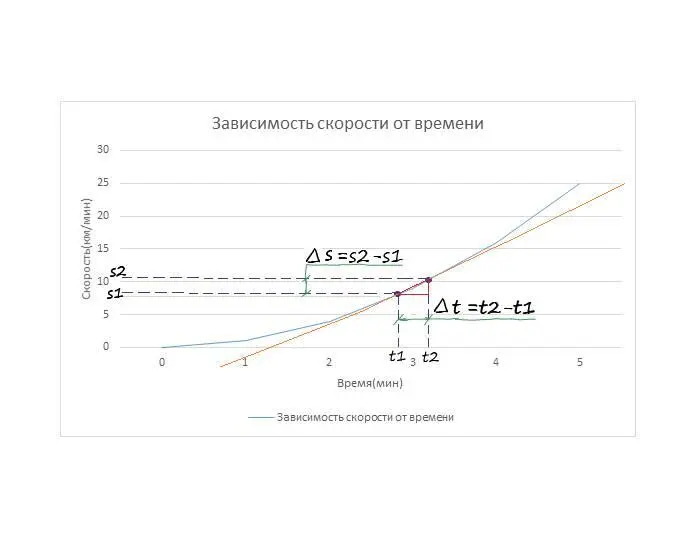
Зная координаты этих точек и проведя проекции по осям, можно вычислить расстояние между этими точками.

Если представить прямоугольный треугольник где гипотенуза – это прямая между двумя точками, а его катеты равны разности проекциям точек по осям (∆t и ∆s), то поделив противолежащий катет на прилежащий получим тангенс угла, который и будет являться коэффициентом крутизны. Зная который, как во втором примере, мы легко определим изменение скорости в момент ∆t.

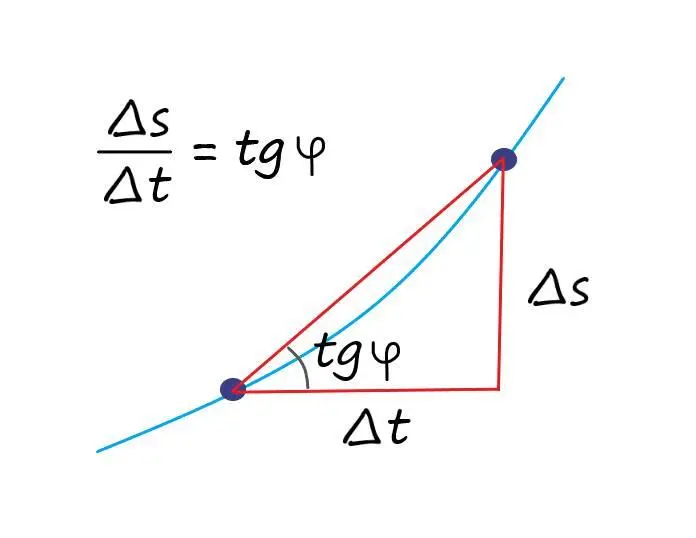
Как мы знаем, скорость изменения – это наклон прямой, которую из второго примера мы уже умеем находить. Значит, около точки (t=3), наш коэффициент крутизны будет равен:

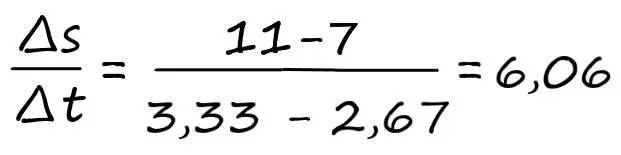
Значит, скорость изменения скорости в момент времени три минуты составляет 6,06 км/мин.

Мы можем говорить о скорости изменения чего угодно – физической величины, экономического показателя и так далее.

Рассмотрим функцию y = f ( x ). Отметим на оси X, некоторое значение аргумента x, а на оси Y– соответствующее значение функции y = f ( x ).

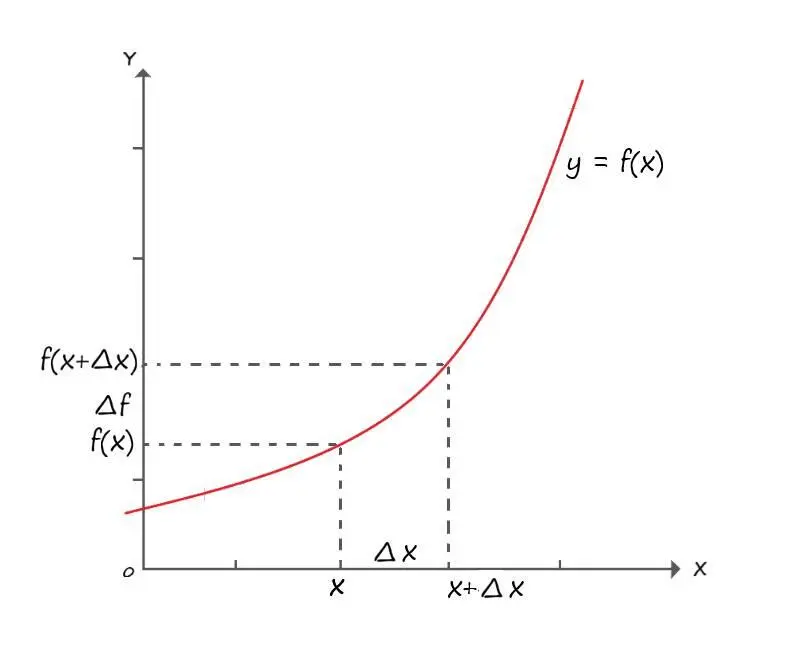
Дадим аргументу x, некоторое приращение, обозначенное как ∆х. Попадаем в точку х+∆х. А соответствующие этим значениям аргументов, значение функции обозначим соответственно f ( x ), ∆ fи f ( x +∆х). Приращение аргумента ∆х, есть аналог промежутка времени ∆ t, а соответствующее приращение функции – это аналог пути ∆ s, пройденного за время ∆ t.

Если представить, что ∆х– бесконечно мала, т.е. стремиться к нулю ( ∆х-›0), то выражение нахождения изменения скорости можно записать как:

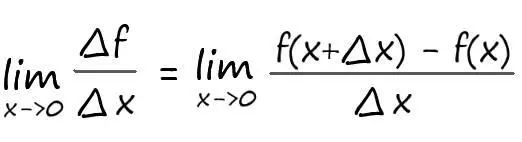
Или исходя из геометрического представления, описанного ранее:

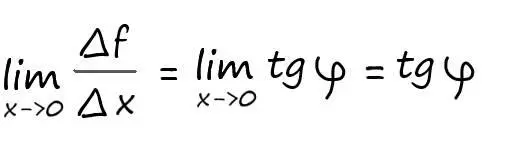
Отсюда вывод, что производная функции f ( x )в точке х– это предел отношения приращения функции к приращению её аргумента, когда приращение аргумента стремиться к нулю.