Каниа Кан - Нейронные сети. Эволюция

Поэтому, при числе входов нейрона, больше одного, наши выработанные до этого правила линейной классификации, необходимо дополнить. Нужно использовать ошибку, чтобы математически связать все входы таким образом, при котором они начнут учитывать общие интересы. И как следствие, на выходе получить нужный классификатор.

Итак, мы постепенно подходим к ключевому понятию в обучении нейрона и нейронных сетей – обучение методом градиентного спуска.

Найдем решение, которое, даже будет не идеальным с точки зрения математики, но даст нам правильные результаты, поскольку всё же опирается на математический инструмент.

Для понимания всего процесса, давайте представим себе спуск с холма, со сложным рельефом. Вы спускаетесь по его склону, и вам нужно добраться до его подножья. Кругом кромешная тьма. У вас в руках есть фонарик, света которого едва хватает на пару метров. Все что вы сможете увидеть, в этом случае – по какому участку, в пределах видимости фонаря, проще всего начать спуск и сможете сделать только один небольшой шаг в этом направлении. Действуя подобным образом, вы будете медленно, шаг за шагом, продвигаться вниз.

У такого абстрактного подхода, есть математическая версия, которая называется – градиентным спуском. Где подножье холма – минимум ошибки, а шагами в его направлении – обновления весовых коэффициентов.

Градиентный спуск – метод нахождения локального минимума или максимума функции с помощью движения вдоль градиента– который, своим направлением указывает направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой, а по величине (модулю) равный скорости роста этой величины в этом направлении.

Метод градиентного спуска позволяет находить минимум, даже не располагая знаниями свойств этой функции, достаточными для нахождения минимума другими математическими методами. Если функция очень сложна, где нет простого способа нахождения минимума, мы в этом случае можем применить метод градиентного спуска. Этот метод может не дать нам абсолютно точного ответа. Но все же это лучше, чем вообще не иметь никакого решения. А его суть, как было описано выше – постепенно приближаться к ответу, шаг за шагом, тем самым медленно, но верно, улучшая нашу позицию.

Для наглядности, рассмотрим использование метода градиентного спуска на простейшем примере.

Возьмём график функции, которая своими значениями иллюстрирует склон. Если бы это была функция ошибки, то нам нужно найти такое значение ( х), которое минимизирует эту функцию:

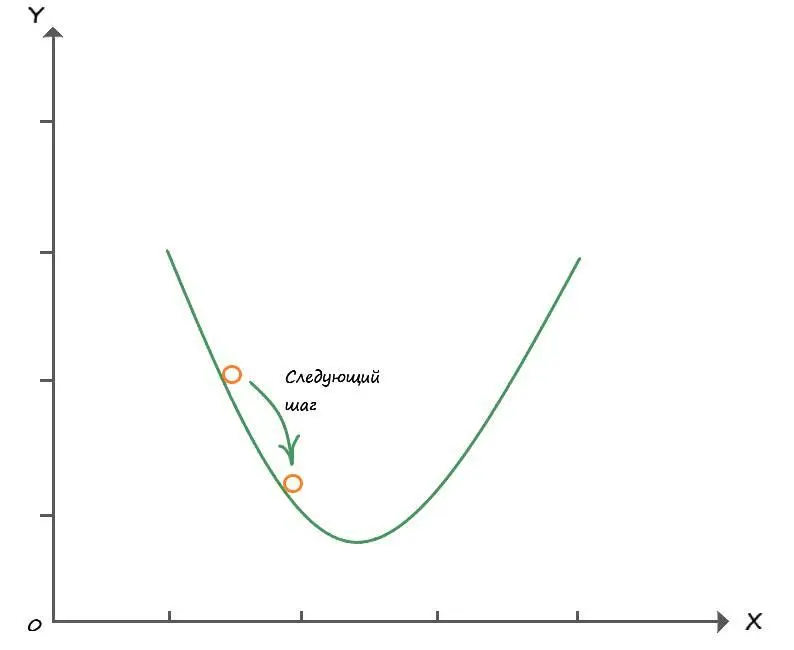
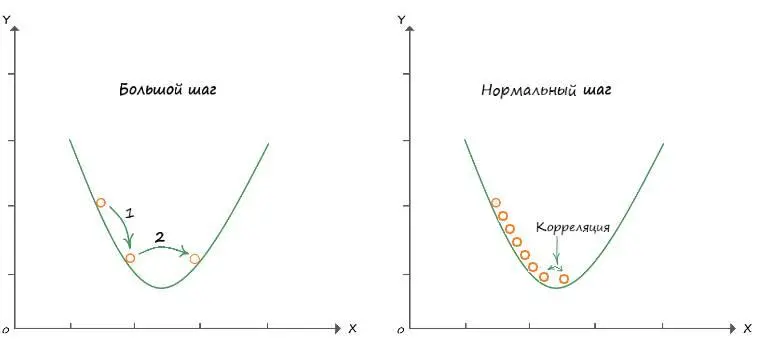
Значение шага (скорости обучения), как мы говорили ранее, играет тоже не малую роль, при слишком большом значении, мы быстро спускаемся, но можем переступить минимум функции – страдает точность. При очень маленьком значении величины скорости обучения, нахождение минимума потребует гораздо больше времени. Нужно подобрать величину шага такой, чтоб он удовлетворяла нас и по скорости, и по точности. При нахождении минимума, наша точка будет коррелировать, возле значения минимум, в чуть большую и меньшую сторону на величину шага. Это все равно что – когда спустившись вплотную к подножью, мы сделали шаг и оказались чуть выше подножья, повернувшись сделали такой же шаг назад, и поняв, что опять находимся чуть выше, повторяли эти действия до бесконечности. Но при этом, мы все равно находились бы очень близко к подножью, потому как величина шага, в общем объеме, ничтожна, поэтому мы можем говорить – что находимся в самом низу.

Выходной сигнал нейрона представляет собой сложную функцию со многими входными данными, и соответствующие им – весовыми коэффициентами связи. Все они коллективно влияют на выходной сигнал. Как при этом подобрать подходящие значения весов используя метод градиентного спуска? Для начала, давайте правильно выберем функцию ошибки.

Функция выходного сигнала не является функцией ошибки. Но мы знаем, что есть связь между этими функциями, поскольку ошибка – это разность между целевыми тренировочными значениями и фактическими выходными значениями ( Е= Y - y).

Однако и здесь не все так гладко. Давайте взглянем на таблицу с тренировочными данными и выходными значениями для трех выходных узлов вместе с разными функциями ошибок:

Функция ошибки, которой мы пользовались ранее ( целевое– выход), не совсем нам подходит, так как можно видеть, что если мы решим использовать сумму ошибок по всем узлам в качестве общего показателя того, насколько хорошо обучена сеть, то эта сумма равна нулю! Нулевая сумма означает отсутствие ошибки. Отсюда следует, что простая разность значений ( целевое– выход), не годится для использования в качестве меры величины ошибки.

Во втором варианте, в качестве меры ошибки используется квадрат разности: (( целевое– выход) ²). Этот вариант предпочтительней первого, поскольку, как видно из таблицы, сумма ошибок на выходе не дает нулевой вариант. Кроме того, такая функция имеет еще ряд преимуществ над первой, делает функцию ошибки непрерывно гладкой, исключая провалы и скачки, тем самым улучшая работу метода градиентного спуска. Еще одно преимущество заключается в том, что при приближении к минимуму градиент уменьшается, что уменьшает корреляцию через точку минимума.

Чтобы воспользоваться методом градиентного спуска, нам нужно применить метод дифференциального исчисления. Не пугайтесь, всё не так сложно, как может показаться.

Дифференциальное исчисление – это просто математически строгий подход к определению величины изменения одних величин при изменении других. Например, мы можем говорить о скорости изменения чего угодно, ускорения или любой другой физической величины, или математической функции.

Не изменяющиеся величина

Если мы представим автомобиль, движущийся с постоянной скоростью в 1,5 км/мин, то отвечая на вопрос, как меняется скорость автомобиля с течением времени, ответ утвердительный никак, ноль, так как его скорость постоянна: