Каниа Кан - Нейронные сети. Эволюция

plt.plot(x,y, label='Начальная прямая', color = 'b')

plt.legend(loc=2) #loc – локация имени, 2 – справа в углу

Метод scatter выводит на плоскость точки с заданными координатами:

plt.scatter(x_data, y_data, color ='g', s=10)

Метод plot выводит на плоскость прямую по заданным точкам:

plt.plot(x, y, 'r')

Ну и наконец отображаем все что натворили, командой plt.show().

Теперь разберем получившийся график. Синим – отмечена начальная прямая, которая изначально не выполняла никакой классификации. После обучения, значение коэффициента A, стабилизируется возле числа = 2.05. Если провести прямую функции y = Ax = 2.05*x, отмеченной красным на графике, то получим значения близкие к нашим входным данным (на графике – зеленые точки).

А что если, наш обученный нейрон смог бы правильно отвечать на вводимые пользователем данные? Если задать условие, что всё что выше красной линии относится к виду – жирафов, а ниже к виду – крокодилов:

x = input("Введите значение ширины Х: ")

x = int(x)

T = input("Введите значение высоты Y: ")

T = int(T)

y = A * x

# Условие

if T > y:

print('Это жираф!')

else:

print('Это крокодил!')

Функция input – принимает значение, вводимое пользователем. А условие гласит: если целевое значение (вводимое пользователем) больше ответа на выходе нейрона (выше красной линии), то сообщаем что – это жираф, иначе сообщаем что – это крокодил.

После ввода наших значений, получаем ответ:

Введите значение ширины Х: 4

Введите значение высоты Y: 15

Это жираф!

Теперь мы можем поздравить себя! Вся наша работа стала сводиться к тому, чтоб просто подавать на вход нейрона данные, не разбираясь в них самостоятельно. Нейрон сам классифицирует их и даст правильный ответ.

Если бы наши действия на работе сводились к подобным классификациям, то у нас появилась бы куча времени на кофе, очень важных общений в социальных сетях, и даже останется время, чтоб разложить пасьянс. И при всем этом можно выполнять ещё больший объём работы, что конечно же должно вознаграждаться премиальными и повышением зарплаты.

Теперь представим, что нам приходит новое задание. Где, проанализировав самостоятельно данные, мы видим, что их координаты значительно отличаются от прежних. Теперь провести классифицирующую прямую, обладая в своем арсенале лишь коэффициентом крутизны – не выйдет!

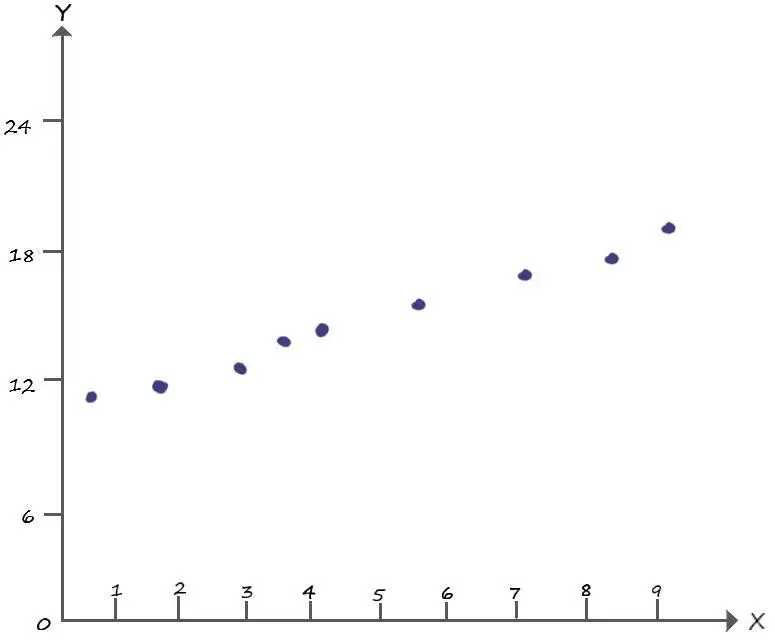
Очевидно, что без параметра b, которого мы до этого избегали ( b=0), тут не обойтись.

Вспомним, что параметр b, в уравнении прямой y = Ax + b, как раз отвечает за точку её пересечения с осью Y. На графике выше, такая точка очевидно находится возле координаты – ( x =0; y =11).

Для того, чтобы выполнить новое задание, придется добавить в наш нейрон, второй вход – отвечающий за параметр b.

Определимся с параметром ( b). Как будет выглядеть второй вход? Какие данные подавать в ходе обучения?

Параметр ( b) – величина постоянная, поэтому мы добавим его на второй вход нейрона, с постоянным значением входного сигнала, равным единице ( x 2 = 1). Таким образом, произведение этого входа на значение величины ( b), всегда будет равно значению самой величины ( b).

Пришло время для первого эволюционного изменения структуры нашего нейрона!

Рассмотрим следующую графическую модель искусственного нейрона:

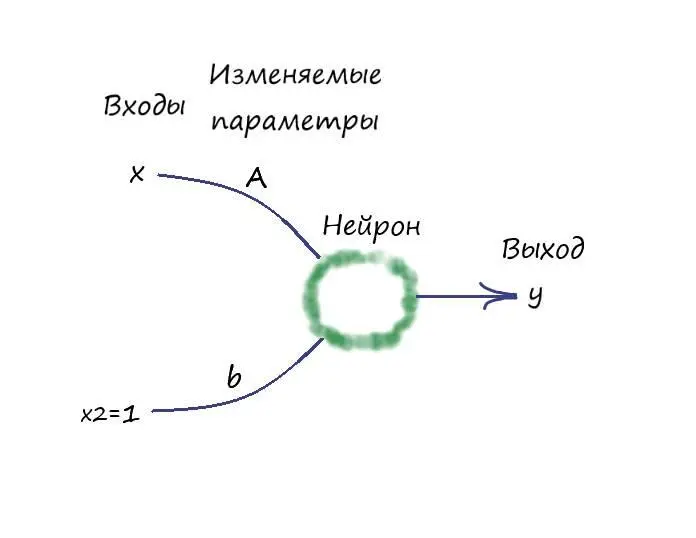
Где, как говорилось выше, на вход нейрона поступают два входных сигнала x(из нашего набора данных) и x 2 = 1. После чего, эти значения умножаются со своими изменяемыми параметрами, а далее они суммируются: A * x + b * x 2. Значение этой суммы, а по совместительству – значение функции y = A * x + b * x 2 = A * x + b, поступает на выход.

Ну и давайте всё представим согласно тем принятым условным обозначениям, которые используются при моделировании искусственных нейронов и нейронных сетей. А именно – коэффициент Аи параметр b, обозначим как w1и w2соответственно. И теперь будем их называть – весовыми коэффициентами.

Ну и конечно же, визуализируем структуру нашего нейрона, с новыми обозначениями:

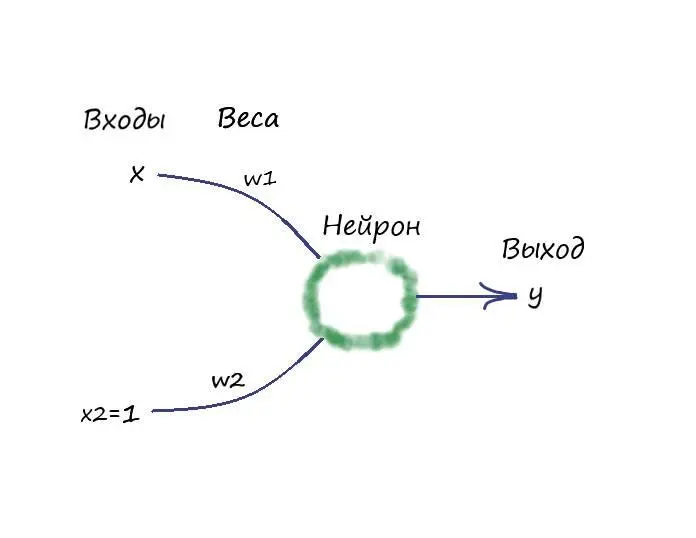
Переименуем в нашей первой программе коэффициент ( А) и параметр ( b), на обозначения весовых коэффициентов, как показано на слайде. Инициализируем их в ней. Дополним небольшую её часть в области с обучением, формулой изменения веса ( w2), как мы это делали ранее с коэффициентом ( А).

После чего, область с обучением в программе, будет выглядеть следующим образом:

# Прогон по выборке

for e in range(epochs):

for i in range(len(arr)): # len(arr) – функция возвращает длину массива

# Получить x координату точки

x = arr[i]

# Получить расчетную y, координату точки

y = w1 * x + w2

# Получить целевую Y, координату точки

target_Y = arr_y[i]

# Ошибка E = целевое значение – выход нейрона

E = target_Y – y

# Меняем вес при входе x

w1 += lr*(E/x)

# Меняем вес при входе x2 = 1, w2 += lr*(E/x2) = lr*E

w2 += lr*E

И забегая вперед, скажу, что тут нас постигнет разочарование – ничего не выйдет…

Дело в том, что вес ( w2) (бывший параметр ( b)), вносит искажение в поправку веса ( w1) (бывшего коэффициента ( А)) и наоборот. Они действуют независимо друг от друга, что сказывается на увеличении ошибки с каждым проходом цикла программы.

Нужен фактор, который заставит наша веса действовать согласованно, учитывать интересы друг друга, идти на компромиссы, ради нужного результата. И такой фактор у нас уже есть – ошибка.

Если мы придумаем как согласованно со всеми входами уменьшать ошибку с каждым проходом цикла в программе, подгоняя под неё весовые коэффициенты таким образом, что в конечном счете привело к самому минимальному её значению для всех входов. Такое решение, являлось бы общим для всех входов нашего нейрона. То есть, согласованно обновляя веса в сторону уменьшения их общей ошибки, мы будем приближаться к оптимальному результату на выходе.