Каниа Кан - Нейронные сети. Эволюция

Запишем в явном виде функцию ошибки, которая представляет собой сумму возведенных в квадрат разностей между целевым и фактическим значениями:

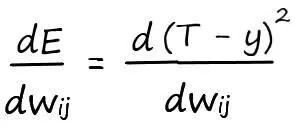
Разобьем пример на более простые части, как мы это делали при дифференцировании сложных функций:

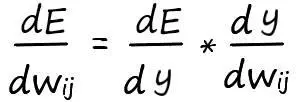
Продифференцируем обе части поочередно:

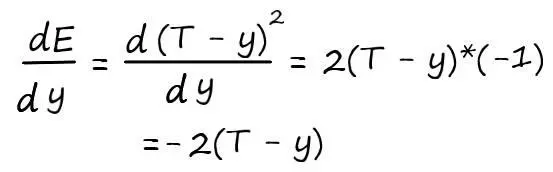
Так как выход нейрона – f(x) = y, а взвешенная сумма – у = ∑ I w ij *x i, где x i– известная величина (константа), а весовые коэффициенты w ij– переменная, производная по которой, дает как мы знаем единицу, то взвешенную сумму можно разбить на сумму простых множителей:

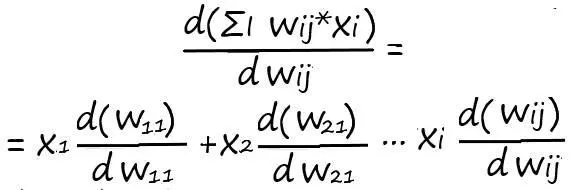
Откуда нетрудно найти:

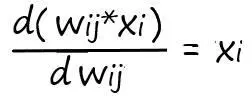
Значит, для того чтобы обновить весовой коэффициент по своей связи:

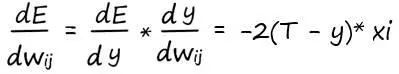
Прежде чем записать окончательный ответ, избавимся от множителя 2 в начале выражения. Мы спокойно можем это сделать, поскольку нас интересует только направление градиента функции ошибки. Не столь важно, какой множитель будет стоять в начале этого выражения, 1, 2 или любой другой (лишь немного потеряем в масштабировании, направление останется прежним). Поэтому для простоты избавимся от неё, и запишем окончательный вид производной ошибки:

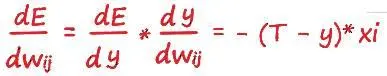
Всё получилось! Это и есть то выражение, которое мы искали. Это ключ к тренировке эволюционировавшего нейрона.

Найдя производную ошибки, вычислив тем самым наклон функции ошибки (подсветив фонариком, подходящий участок для спуска), нам необходимо обновить наш вес в сторону уменьшения ошибки (сделать шаг в сторону подсвеченного фонарем участка). Затем повторяем те же действия, но уже с новыми (обновлёнными) значениями.

Для понимания как мы будем обновлять наши коэффициенты (делать шаги в нужном направлении), прибегнем к помощи так уже нам хорошо знакомой – иллюстрации. Напомню, величина шага зависит от крутизны наклона прямой (tgφ). А значит величина, на которую мы обновляем наши веса, в соответствии со своим входом, и будет величиной производной по функции ошибки:

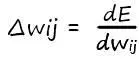
Вот теперь иллюстрируем:

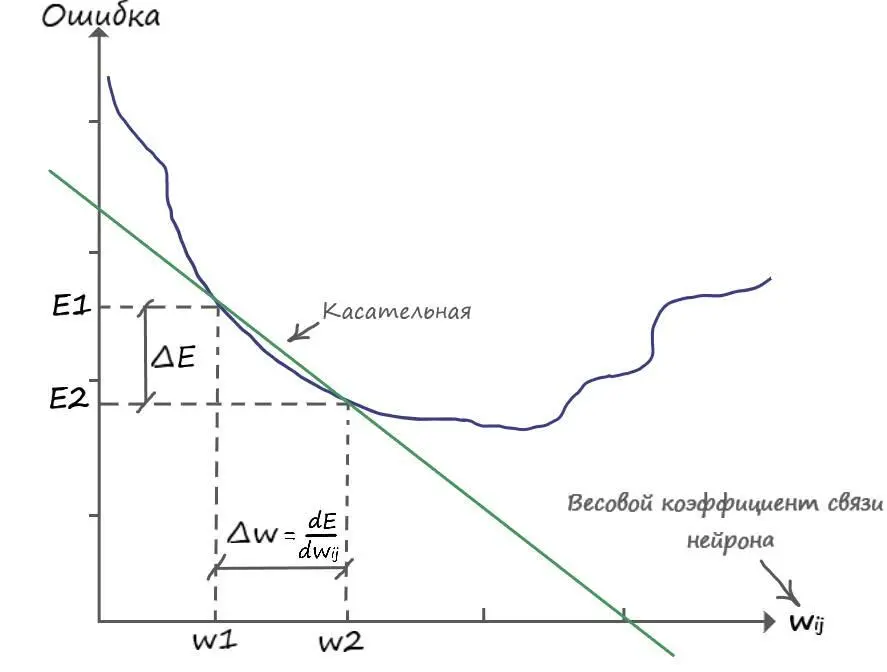
Из графика видно, что для того чтобы обновить вес в большую сторону, до значения ( w2), нужно к старому значению ( w1) прибавить дельту ( ∆w), откуда: ( w2 = =w1+∆w). Приравняв ( ∆w) к производной ошибки (величину которой уже знаем), мы спускаемся на эту величину в сторону уменьшения ошибки.

Так же замечаем, что ( E 2 – E 1 = -∆ E) и ( w 2 – w 1 = ∆ w), откуда делаем вывод:

∆ w = -∆ E /∆ w

Ничего не напоминает? Это почти то же, что и дельта линейного классификатора ( ∆А = E/х), подтверждение того что наша эволюция прошла с поэтапным улучшением математического моделирования. Таким же образом, как и с обновлением коэффициента ( А = А+∆А), линейного классификатора, обновляем весовые коэффициенты:

новый w ij = старый w ij -( – ∆ E /∆ w )

Знак минус, для того чтобы обновить вес в большую сторону, для уменьшения ошибки. На примере графика – от w1до w2.

В общем виде выражение записывается как:

новый w ij = старый w ij – dE/ dw ij

Еще одно подтверждение, постепенного, на основе старого аппарата, хода эволюции, в сторону улучшения классификации искусственного нейрона.

Теперь, зайдем с другой стороны функции ошибки:

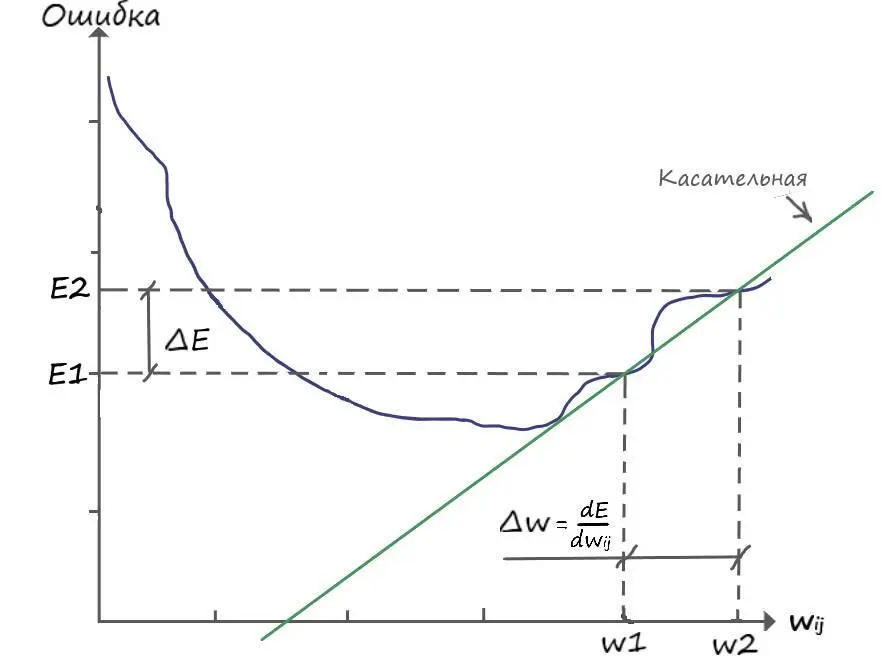
Снова замечаем, что ( E 2 – E 1 = ∆ E) и ( w 2 – w 1 = ∆ w), откуда делаем вывод:

∆ w = ∆ E /∆ w

В этом случае, для обновления весового коэффициента, в сторону снижения функции ошибки, а значит до значения находящееся левее ( w1), необходимо от значения ( w1) вычесть дельту ( ∆w):

новый w ij = старый w ij - ∆ E /∆ w

Получается, что независимо от того, какого знака производная ошибки от весового коэффициента по входу, вычитая из старого значения – значение этой производной, мы движемся в сторону уменьшения функции ошибки. Откуда можно сделать вывод, что последнее выражение, общее для всех возможных случаев обновления градиента.

Запишем еще раз, обновление весовых коэффициентов в общем виде:

новый w ij = старый w ij – dE/ dw ij

Но мы забыли еще об одной важной особенности… Сглаживания! Без сглаживания величины дельты обновления, наши шаги будут слишком большие. Мы подобно кенгуру, будем прыгать на большие расстояния и можем перескочить минимум ошибки! Используем прошлый опыт, чтоб устранить этот недочёт.

Вспоминаем старое выражение при нахождении сглаженного значения дельты линейного классификатора: ∆А = L*(Е/х). Где ( L) – скорость обучения, необходимая для того, чтобы мы делали спуск, постепенно, небольшими шашками.

Ну и наконец, давайте запишем окончательный вариант выражения при обновлении весовых коэффициентов:

новый w ij = старый w ij – L *( dE/ dw ij )