Каниа Кан - Нейронные сети. Эволюция

Значение – у = 10,5, далеко от значения y = 39.

Ну и давайте снова предпримем все те действия, что делали для нахождения параметров разделяющей линии в первом примере, только уже для второго значения из нашей таблицы.

Е = T – y = 39 – 10,5 = 28,5

Теперь параметр ∆Апримет следующее значение:

∆А = Е/х = 28,5 / 20 = 1,425

Обновим коэффициент крутизны А:

А = А+ ∆А = 0,525 +1,425 = 1,95

Получим обновленный ответ:

y = А х = 1,95 * 20 = 39

То есть, при x = 20, A = 1,95и ∆А = 1,425– функция возвращает в качестве ответа значение 39, которое и является желаемым целевым значением.

Представим все наши действия на графике:

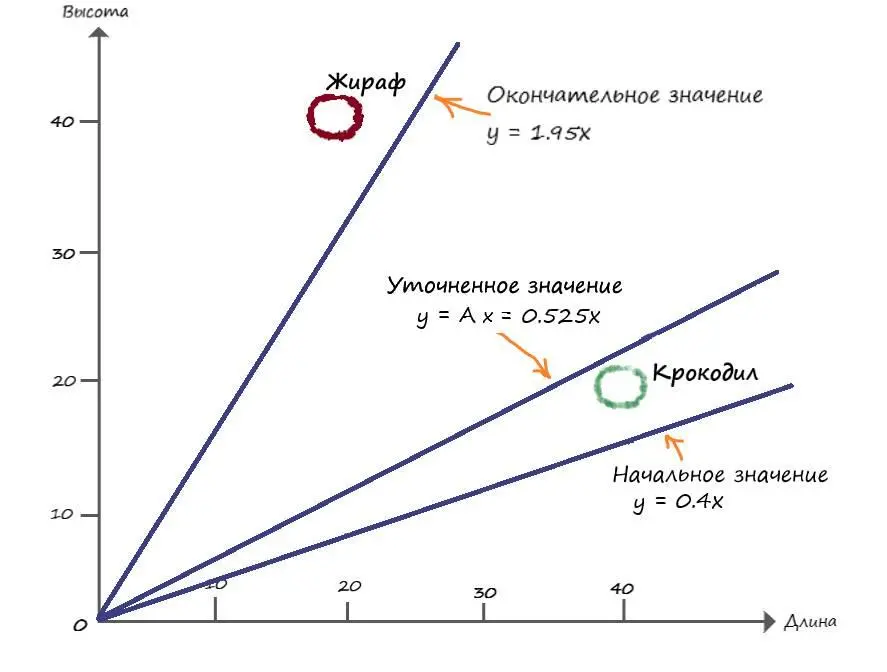
Теперь мы наблюдаем, что линия разделила два вида, исходя из табличных значений. Но полученная нами разделяющая линия лежит гораздо выше её воображаемого центра, к которому мы стремимся:

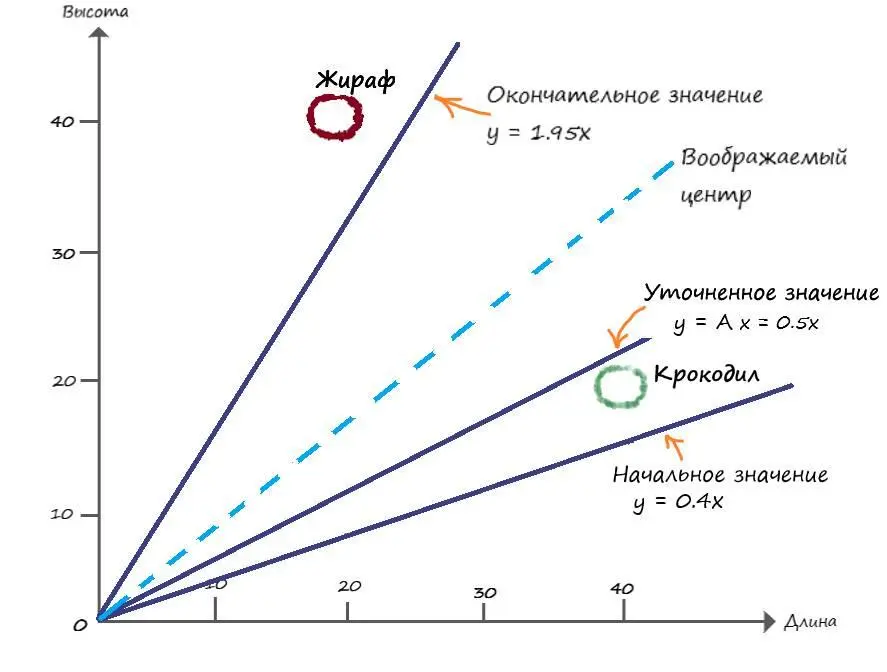
Но и это легко поправимо. Мы добьемся желаемого результата сглаживая обновления, через специальный коэффициент сглаживания – L, который часто называют как – скорость обучения.

Суть идеи: что каждый раз обновляя А, мы будем использовать лишь некоторую долю этого обновления. За счет чего, с каждым тренировочным примером, мы мелкими шагами будем двигаться в нужную нам сторону, и в конечном результате остановимся около воображаемой прямой по центру.

Давайте сделаем такой перерасчет:

∆А = L * (Е / X)

Выберем L =0,5в качестве начального приближения. То есть, мы будем использовать поправку вдвое меньшей величины, чем без сглаживания.

Повторим все расчеты, используя начальное значение А=0,4. Первый тренировочный пример дает нам у = Ax = О,4 * 40 = 16. При x = 40и коэффициенте А = 0,4, ошибка E = T – y = 21 – 16 = 5. Чтобы график прямой, не проходил через точку с нашими координатами, а проходил выше её, то принимаем целевое значение – T = 21.

Рассчитаем поправку: ∆А = L (Е / х) = 0,5*(5 / 40) = 0,0625. Обновленное значение: А = A + ∆А = 0,4 + 0,0625= 0,4625.

Сглаженное уточнение: y = Ax = 0,4625 * 40 = 18,5.

Теперь перейдем к расчетам следующего тренировочного примера.

Используя обновлённое на первом прогоне значение А, для второго тренировочного примера у = Ax = О,4625 * 20 = 9,25.

Значение, у = 9,25– всё так же далеки от значения y = 39, но мы все равно движемся в нужном направлении, но уже с меньшой скоростью.

При x = 20и коэффициенте А = 0, 4625, ошибка E = T – y = 39 – 9,25 = 29,75. Так как мы хотим, чтобы график прямой, не проходил через точку с нашими координатами, а проходил ниже её, то принимаем целевое значение – T = 39. Рассчитаем поправку ∆А = L (Е / х) = 0,5*(29,75 / 20) = 0,74375. Обновлённое значение А = A + ∆А = 0,4625+ 0,74375 = 1,20625.

Сглаженное уточнение y = = Ax = 1,20625 * 20 = 24,125.

Теперь еще раз отобразим на координатной диаграмме, начальный, улучшенный и окончательный варианты разделительной линии:

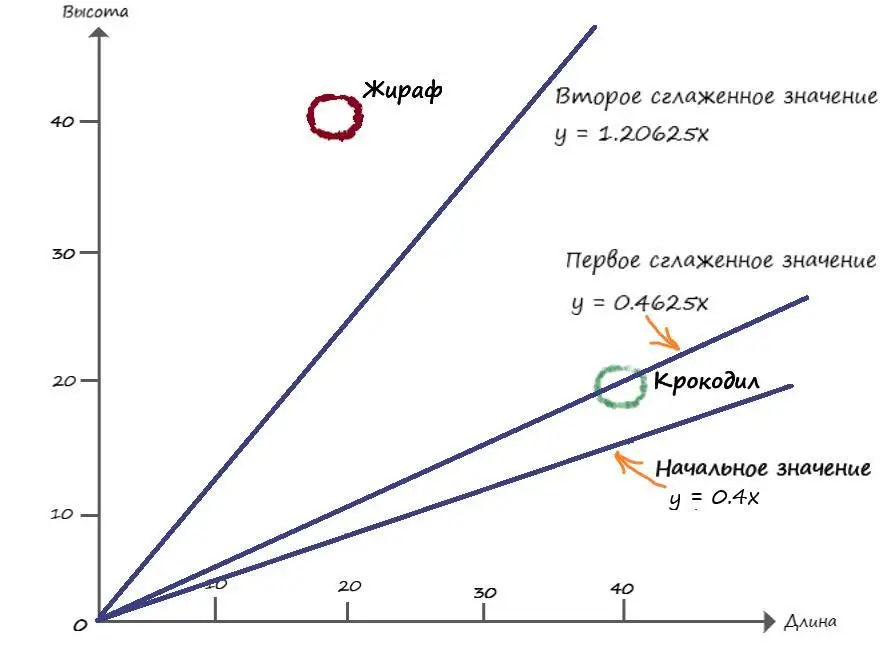
Можно убедиться в том, что сглаживание обновлений приводит к более удовлетворительному расположению разделительной линии.

Если еще уменьшить скорость обучения Lи повторить расчеты с первым и вторым обучающим примером, то в итоге наша разделительная линия окажется очень близко к воображаемой линии.

Применяя способ уменьшение величины обновлений с помощью коэффициента скорости обучения, ни один из пройденных тренировочных примеров, не будет доминировать в процессе обучения.

В этой главе мы будем создавать собственные нейронные сети. Сначала создадим модель работы искусственного нейрона, а затем научимся моделировать сеть из множества нейронов.

При моделировании нейронных сетей, мы будем использовать язык программирования Python.

Почему Python? Он очень прост в освоении, кроме того, нейронные сети создают и обучают в основном на этом языке. Кроме того, Python очень популярный и распространённый язык программирования.

О Python, можно рассказывать долго и много, но мы будем изучать Python лишь в том объеме, который необходим для достижения нашей цели – изучить работу нейронных сетей.

Посетите сайт – http://www.continuum.io/downloads, на котором предлагаются различные варианты установки Anaconda Python. Я использую пакет Anaconda, для операционной системы Windows, вы можете выбрать другие варианты – OS X или Linux. Пакет Anaconda предоставляет удобное средство интерактивной разработки Jupyter Notebook, в котором необычайно удобно писать и проверять программный код. На момент написания книги, доступен пакет Anaconda 5.0.1, и Python 3.6 – который и рекомендую установить.

Если, к тому времени, когда вы посетите сайт, все будет выглядеть иначе, не пугайтесь, сути дела это не поменяет.

После установки пакета Anaconda, запустите интерактивную оболочку Jupyter Notebook, нажмите на кнопку New у правого края окна и выберите в открывшемся меню пункт Python 3, что приведет к открытию пустого блокнота:

Переменные

В переменных всегда что-то хранится (число, объекты, символы, строки). Попробуем создать переменную x со значением 20. И выведем это значение, на экран, при помощи функции – print(). Функция print() – выводит на консоль то, что расположено между её скобками:

С переменными, которые хранят числа, можно выполнять различные простейшие действия: складывать, вычитать, умножать, делить и возводить в степень:

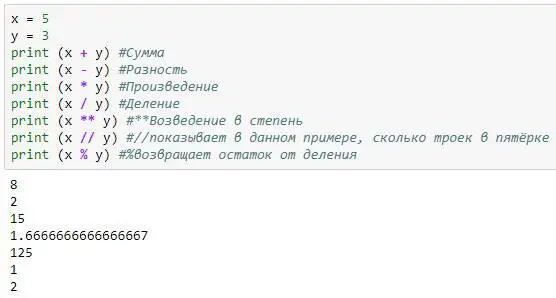
Справа от функции print(), вы можете видеть комментарии. Делаются они очень просто, для этого, перед комментарием, необходимо поставить знак #, и текст после этого знака, в данной строке, Pytnon будет воспринимать, не как программный код, а как обычную текстовую область.