А. Степанов - Число и культура

a ~ c

b ~ ( 0,618 a – b)

a + b = c .

После стандартных преобразований получим теоретическую цифру а/с  0,786 = 78,6%.

На деле представители демократических партий в Испании собрали 34,8 + 30,3 = 65,1% голосов. У сторонников тоталитарных партий – 9,3 + 8,4 = 17,7%. Следовательно, доля первой группы составляет а/с = 65,1 / (65,1 + 17,7) = 78,6%, полное соответствие теории.

Теперь сравним полные кватерниорные паттерны: расчетный и действительный, – как это уже делалось ранее. Для получения теоретической картины необходимо взять две формообразующие пропорции: а/с = 53,6% (соответственно, b/c = 46,4%) и а/с = 78,6% ( b/c = 21,4%), – и построить из них разделенный на четыре части квадрат со сторонами по 100%:

Площади четырех прямоугольников – образы электоральных объемов поименованных партий, выраженных в процентах. Для адекватного представления того, что получилось на практике, следует взять реальные цифры (их сумма, см. выше, равна 82,8%) и произвести нормировку к 100% (действительные величины – разделить на 0,828). Как и прежде, воспользуемся графическим способом представления данных по правилам геометрической алгебры:

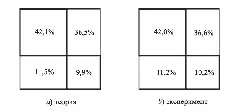
Соответствие расчетных величин реальным, по-видимому, удовлетворительно: расхождения – в десятых долях процента. Если согласиться, что в 1977 г. Испании еще не хватало непосредственного политического опыта в новых условиях, то здравый смысл ей был присущ в полной мере, включая сферу политики, – не только на сознательном, но и бессознательном уровне. Рациональное бессознательное сработало с точностью калькулятора. В подобных случаях в политологии говорят об установлении политического равновесия, или баланса, дискутируя лишь о его природе: равновесие то ли устанавливается автоматически, то ли обязано целенаправленной деятельности заинтересованных политических лидеров [198, c. 151]. К счастью, в рамках нашего подхода такая разграничительная линия не востребована: рациональные сознание и бессознательное в социуме действуют солидарно и неразрывно. Испания в 1977 г. представила один из интересных образцов самосогласованного (а значит, устойчивого) демократического паттерна, когда определенные начала гармонии воплотились в народной душе как идеал, к которому следует последовательно стремиться. По замечанию исследователя, парламентские выборы, состоявшиеся через два года, в 1979 г., "почти ничего не изменили ни в расстановке политических сил, ни даже в объемах голосования за отдельные партии" [101, c. 111], что избавляет нас от необходимости новых расчетов.

Чтобы убедиться, что феномен "производных" пропорций, надстроенных над каноническими, – не случайность, полезно воспользоваться еще одной иллюстрацией. Конечно, не только золотому сечению, но и пропорции 1 : √3 иногда удается сыграть роль отправной, или исходной. Что произойдет, если один из членов конкурирующей политической пары имплицитно выберет для себя в качестве образца лидера из "жесткой гонки" (или, что численно то же, "благодушного соревнования", любого другого подходящего герменевтического варианта), тогда как второй займет самую распространенную из установок преследователя: b тянется за фаворитом а ? В этом случае, очевидно

a ~ (1/√3) c

( 29 )

b ~ a

a + b = c .

Чтобы сэкономить место, пропустим алгебраические преобразования и приведем окончательный результат:

а/с  0,524 = 52,4%.

( 30 )

Соответственно, b/c составляет 47,6%.

Первая строчка (29) – очередная разновидность так называемых сложных, или производных, условий, берущая истоки в школьной математике. Возможно, это еще не забыто: если z есть функция от y , а y , в свою очередь, – функция от x , то функция f(x) = z [ y(x) ] называется сложной функцией или композицией функций от x . В конкретном случае, определенная совокупность условий, например (14) или (17), приводила к решению 1 : √3. Это отношение – один из самых прочных и ключевых атрибутов коллективного сознания или бессознательного. Отталкиваясь от него как от основы, надстраивается второй этаж, т.е. берется функция от функции, равенство превращается в пропорциональность. Выше аналогичной процедуре были подвергнуты и золотое сечение, и величина 1/3.

Как и обещано, не станем препарировать самые тривиальные случаи соревнований двух акторов (процент, близкий к 52,4, встречается вовсе не редко)(3) и сразу обратимся к политическому кватерниону. Заодно разбавим стройный ряд, составленный из посттоталитарных социумов, и взглянем на Нидерланды.

По результатам выборов в нижнюю палату парламента в 1994 г. ведущие позиции достались четырем партиям: Рабочей партии (37 мест), христианским демократам (34 места), либералам (21) и "Демократам- 66" (24 места), см. [167, c. 167]. Ближайшие преследователи четверки заметно отстали: у "Старшего поколения" – всего 7 мандатов, у "зеленых" – 5, у остальных – еще меньше. Этот факт, а также репрезентативность четверки (она покрывала собой более трех четвертей общего состава парламента) позволяют предположить, что политическое лицо голландского общества в данный период определяла именно она. Рабочая партия, либералы и "Демократы' 66" объединились в правительственную коалицию (у коалиции, кстати, – 61,3% от общего количества мест, ср. золотое деление, но это вряд ли в состоянии удивить, поэтому на сей раз занимаемся более тонкими соотношениями). Выясним пропорции внутри ведущей четверки.

Четыре фактические цифры: 37, 34, 24, 21 (количества мандатов), – могут быть представлены тем же способом, что и прежде. Целое с равно их сумме: с = 116. Распределение процентных долей имеет следующий вид:

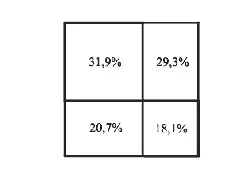
Верхняя левая цифра отвечает удельному весу Рабочей партии, правая – христианских демократов. Внизу слева – относительный электоральный объем "Демократов- 66" и справа – либералов. В одном из планов картина довольно типичная для Европы: основная борьба за голоса избирателей развернулась между разновидностью социалистических сил, Рабочей партией, и представителями умеренно правых, христианскими демократами. Они заняли в общем зачете первое и второе места, оторвавшись от остальных. Однако, в отличие от тривиальной биполярности, названной оппозиции принадлежит здесь хотя и доминирующая, но не подавляющая роль. На долю двух ведущих партий пришлось 31,9 + 29,3 = 61,2% голосов в составе ведущей четверки, что вновь заставляет вспомнить о закономерности золотого сечения и позволяет предположить: население действительно полагало Рабочую партию и христианских демократов "главными" партиями, но при этом и совокупности остальных (либералам и "Демократам- 66") удавалось составить конкуренцию первым, следуя за ними пусть не по пятам, но и без фатального отставания. С подобными ситуациями мы уже знакомы, и более любопытным кажется соотношение между парами в другом направлении.