Дмитрий Гусев - Краткий курс логики: Искусство правильного мышления

Частный объём субъекта и отрицательная связка суждений вида O обусловливают то, что в них субъект и предикат, так же как и в суждениях вида I , могут быть только в отношениях пересечения и подчинения. Читатель без труда сможет подобрать примеры суждений вида O , в которых субъект и предикат находятся в этих отношениях.

1. Что такое простое суждение?

2. На каком основании простые суждения подразделяются на виды? Почему они делятся именно на четыре вида?

3. Охарактеризуйте все виды простых суждений: название, структура, условное обозначение. Придумайте пример для каждого из них. К каким суждениям – общим или частным – относятся суждения с единичным объёмом субъекта?

4. Откуда взяты буквы для обозначения видов простых суждений?

5. В каких отношениях могут быть субъект и предикат в каждом из видов простых суждений? Подумайте, почему в суждениях вида A субъект и предикат не могут пересекаться или быть несовместимыми? Почему в суждениях вида I субъект и предикат не могут находиться в отношениях равнозначности или несовместимости? Почему в суждениях вида E субъект и предикат не могут быть равнозначными, пересекающимися или подчинёнными? Почему в суждениях вида O субъект и предикат не могут находиться в отношении равнозначности или несовместимости? Изобразите кругами Эйлера возможные отношения между субъектом и предикатом во всех видах простых суждений.

Терминами сужденияназываются его субъект и предикат.

Термин считается распределённым(развёрнутым, исчерпанным, взятым в полном объёме), если в суждении речь идёт обо всех объектах, входящих в объём этого термина. Распределённый термин обозначается знаком «+», а на схемах Эйлера изображается полным кругом (кругом, который не содержит в себе другого круга и не пересекается с другим кругом) (рис. 22).

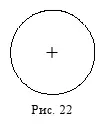
Термин считается нераспределённым(неразвёрнутым, неисчерпанным, взятым не в полном объёме), если в суждении речь идёт не обо всех объектах, входящих в объём этого термина. Нераспределённый термин обозначается знаком «–», а на схемах Эйлера изображается неполным кругом (кругом, который содержит в себе другой круг (рис. 23, a ) или пересекается с другим кругом (рис. 23, б ).

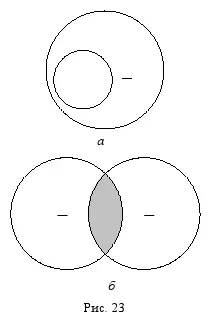
Например, в суждении: « Все акулы (S) являются хищниками (Р) », – речь идёт обо всех акулах, значит, субъект этого суждения распределён.

Однако в данном суждении речь идёт не обо всех хищниках, а только о части хищников (именно о тех, которые являются акулами), следовательно, предикат указанного суждения нераспределён. Изобразив отношения между субъектом и предикатом (которые находятся в отношении подчинения) рассмотренного суждения схемами Эйлера, увидим, что распределённому термину (субъекту « акулы ») соответствует полный круг, а нераспределённому (предикату « хищники ») – неполный (попадающий в него круг субъекта как бы вырезает из него какую-то часть):

Распределённость терминов в простых суждениях может быть различной в зависимости от вида суждения и характера отношений между его субъектом и предикатом. В табл. 4 представлены все случаи распределённости терминов в простых суждениях:

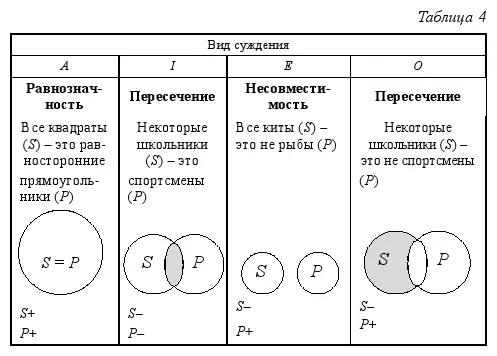
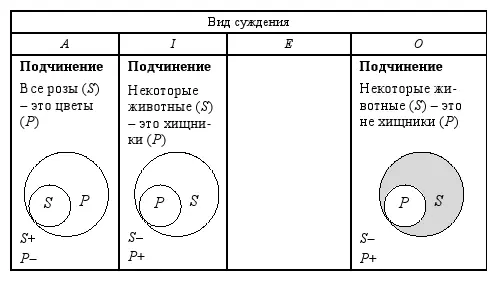
Здесь рассмотрены все четыре вида простых суждений и все возможные случаи отношений между субъектом и предикатом в них (см. раздел 2. 2). Обратите внимание на суждения вида O , в котором субъект и предикат находятся в отношении пересечения. Несмотря на пересекающиеся круги на схеме Эйлера, субъект данного суждения нераспределён, а предикат распределён. Почему так получается? Выше мы говорили о том, что пересекающиеся на схеме круги Эйлера обозначают нераспределённые термины. Штриховкой показана та часть субъекта, о которой идёт речь в суждении (в данном случае – о школьниках, которые спортсменами не являются), в силу чего круг, обозначающий на схеме Эйлера предикат, остался полным (круг, обозначающий субъект, не отрезает от него какую-то часть, как это происходит в суждении вида I , где субъект и предикат находятся в отношении пересечения).

Итак, мы видим, что субъект всегда распределён в суждениях вида A и E и всегда не распределён в суждениях вида I и O , а предикат всегда распределён в суждениях вида E и O , но в суждениях вида A и I он может быть как распределённым, так и нераспределённым в зависимости от характера отношений между ним и субъектом в этих суждениях.

Проще всего устанавливать распределённость терминов в простых суждениях с помощью схем Эйлера (все случаи распределённости из таблицы запоминать совсем не обязательно). Достаточно уметь определять вид отношений между субъектом и предикатом в предложенном суждении и изображать их круговыми схемами. Далее ещё проще – полный круг, как уже говорилось, соответствует распределённому термину, а неполный – нераспределённому. Например, требуется установить распределённость терминов в суждении: « Некоторые русские писатели – это всемирно известные люди ». Сначала найдём в этом суждении субъект и предикат: « русские писатели » – субъект, « всемирно известные люди » – предикат. Теперь установим, в каком они отношении. Русский писатель может как быть, так и не быть всемирно известным человеком, и всемирно известный человек может как быть, так и не быть русским писателем, следовательно, субъект и предикат указанного суждения находятся в отношении пересечения. Изобразим это отношение на схеме Эйлера, заштриховав ту часть, о которой идёт речь в суждении (рис. 25):

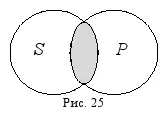
И субъект, и предикат изображаются неполными кругами (у каждого из них как бы отрезана какая-то часть), следовательно, оба термина предложенного суждения нераспределены ( S –, P –).

Рассмотрим ещё один пример. Надо установить распределённость терминов в суждении: « Некоторые люди – это спортсмены ». Найдя в этом суждении субъект и предикат: « люди » – субъект, « спортсмены » – предикат, и установив отношение между ними – подчинение, изобразим его на схеме Эйлера, заштриховав ту часть, о которой идёт речь в суждении (рис. 26):