Дмитрий Гусев - Краткий курс логики: Искусство правильного мышления

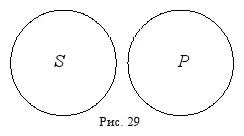
На круговой схеме видно, что и субъект, и предикат распределены (и тому, и другому термину соответствует полный круг), следовательно, мы должны сопроводить как субъект, так и предикат квантором « все ». После этого совершим обращение с суждением: « Все акулы не являются не рыбами ». Получится: « Все не рыбы не являются акулами ». Суждение звучит непривычно, однако это – более короткая формулировка той мысли, что если какое-то существо не является рыбой, то оно никак не может быть акулой, или что все существа, которые не являются рыбами, автоматически не могут быть и акулами в том числе. Обращение можно было сделать и проще, посмотрев в табл. 5 для обращения, которая приведена выше. Увидев, что суждение вида E всегда обращается в само себя, мы могли, не используя круговой схемы и не устанавливая распределённости терминов, сразу поставить перед предикатом « не рыбы » квантор « все ». В данном случае был предложен другой способ, чтобы показать, что вполне можно обойтись без табл. для обращения, и запоминать её совсем необязательно. Здесь происходит примерно то же самое, что и в математике: можно запоминать различные формулы, но можно обойтись и без запоминания, т. к. любую формулу нетрудно вывести самостоятельно.

Все три операции преобразования простых суждений проще всего совершать с помощью круговых схем. Для этого надо изобразить три термина: субъект, предикат и понятие, противоречащее предикату (непредикат). Потом следует установить их распределённость, и из получившейся схемы Эйлера будут вытекать четыре суждения – одно исходное и три результата преобразований. Главное, помнить, что распределённый термин соответствует квантору « все », а нераспределённый – квантору « некоторые »; что соприкасающиеся на схеме Эйлера круги соответствуют связке « является », а несоприкасающиеся – связке « не является ». Например, требуется совершить три операции преобразования с суждением: « Все учебники являются книгами ». Изобразим субъект « учебники », предикат « книги » и непредикат « не книги » круговой схемой и установим распределённость этих терминов (рис. 30):

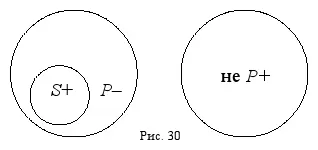
Получившуюся круговую схему можно прочитать четырьмя способами:

1. Все учебники являются книгами (исходное суждение).

2. Некоторые книги являются учебниками (обращение).

3. Все учебники не являются не книгами (превращение).

4. Все не книги не являются учебниками (противопоставление предикату).

Рассмотрим ещё один пример. Надо преобразовать тремя способами суждение: « Все планеты не являются звёздами ». Изобразим кругами Эйлера субъект « планеты », предикат « звёзды » и непредикат « не звёзды ». Обратите внимание на то, что понятия « планеты » и « не звёзды » находятся в отношении подчинения: планета – это обязательно не звезда, но небесное тело, которое не является звездой – это не обязательно планета. Установим распределённость этих терминов (рис. 31):

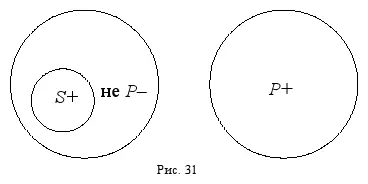
Получившуюся круговую схему можно прочитать четырьмя разными способами:

1. Все планеты не являются звёздами (исходное суждение).

2. Все звёзды не являются планетами (обращение).

3. Все планеты являются не звёздами (превращение).

4. Некоторые не звёзды являются планетами (противопоставление предикату).

1. Каким образом осуществляется операция обращения? Возьмите три каких-нибудь суждения и произведите с каждым из них обращение. Как происходит обращение во всех видах простых суждений и во всех случаях отношений между их субъектом и предикатом? Какие суждения не поддаются обращению?

2. Что такое превращение? Возьмите три любых суждения и совершите с каждым из них операцию превращения.

3. Что представляет собой операция противопоставления предикату? Возьмите три каких-нибудь суждения и преобразуйте каждое из них путём противопоставления предикату.

4. Каким образом знания о распределённости терминов в простых суждениях и умение её устанавливать с помощью круговых схем может помочь в проведении операций преобразования суждений?

5. Возьмите какое-нибудь суждение вида A и совершите с ним все операции преобразования с помощью круговых схем и установления распределённости терминов. Сделайте то же самое с каким-нибудь суждением вида E .

Простые суждения делятся на сравнимые и несравнимые.

Сравнимые (идентичные по материалу)суждения имеют одинаковые субъекты и предикаты, но могут отличаться кванторами и связками. Например, суждения: « Все школьники изучают математику », « Некоторые школьники не изучают математику », – являются сравнимыми: у них совпадают субъекты и предикаты, а кванторы и связки различаются. Несравнимыесуждения имеют разные субъекты и предикаты. Например, суждения: « Все школьники изучают математику », « Некоторые спортсмены – это олимпийские чемпионы », – являются несравнимыми: субъекты и предикаты у них не совпадают.

Сравнимые суждения бывают, как и понятия, совместимыми и несовместимыми и могут находиться в различных отношениях между собой.

Совместимыминазываются суждения, которые могут быть одновременно истинными. Например, суждения: « Некоторые люди – это спортсмены », « Некоторые люди – это не спортсмены », – являются одновременно истинными и представляют собой совместимые суждения.

Несовместимыминазываются суждения, которые не могут быть одновременно истинными: истинность одного из них обязательно означает ложность другого. Например, суждения: « Все школьники изучают математику», «Некоторые школьники не изучают математику », – не могут быть одновременно истинными и являются несовместимыми (истинность первого суждения с неизбежностью приводит к ложности второго).

Совместимые суждения могут находиться в следующих отношениях:

1. Равнозначность– это отношение между двумя суждениями, у которых и субъекты, и предикаты, и связки, и кванторы совпадают. Например, суждения: « Москва является древним городом »,

« Столица России является древним городом », – находятся в отношении равнозначности.

2. Подчинение– это отношение между двумя суждениями, у которых предикаты и связки совпадают, а субъекты находятся в отношении вида и рода. Например, суждения: « Все растения являются живыми организмами », « Все цветы (некоторые растения) являются живыми организмами », – находятся в отношении подчинения.