Дмитрий Гусев - Краткий курс логики: Искусство правильного мышления

3. Частичное совпадение (субконтрарность)– это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения: « Некоторые грибы являются съедобными », « Некоторые грибы не являются съедобными », – находятся в отношении частичного совпадения. Необходимо отметить, что в этом отношении находятся только частные суждения – частноутвердительные ( I ) и частноотрицательные ( O ).

Несовместимые суждения могут находиться в следующих отношениях.

1. Противоположность (контрарность)– это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения: « Все люди являются правдивыми », « Все люди не являются правдивыми », – находятся в отношении противоположности. В этом отношении могут быть только общие суждения – общеутвердительные ( A ) и общеотрицательные ( E ). Важным признаком противоположных суждений является то, что они не могут быть одновременно истинными, но могут быть одновременно ложными. Так, два приведённых противоположных суждения не могут быть одновременно истинными, но могут быть одновременно ложными: неправда, что все люди являются правдивыми, но также неправда, что все люди не являются правдивыми.

Противоположные суждения могут быть одновременно ложными, потому что между ними, обозначающими какие-то крайние варианты, всегда есть третий, средний, промежуточный вариант. Если этот средний вариант будет истинным, то два крайних окажутся ложными. Между противоположными (крайними) суждениями: « Все люди являются правдивыми », « Все люди не являются правдивыми », – есть третий, средний вариант: « Некоторые люди являются правдивыми, а некоторые не являются таковыми », – который, будучи истинным суждением, обусловливает одновременную ложность двух крайних, противоположных суждений.

2. Противоречие (контрадикторность)– это отношение между двумя суждениями, у которых предикаты совпадают, связки различны, а субъекты отличаются своими объёмами, т. е. находятся в отношении подчинения (вида и рода). Например, суждения: « Все люди являются правдивыми», «Некоторые люди не являются правдивыми» , – находятся в отношении противоречия. Важным признаком противоречащих суждений, в отличие от противоположных, является то, что между ними не может быть третьего, среднего, промежуточного варианта. В силу этого два противоречащих суждения не могут быть одновременно истинными и не могут быть одновременно ложными: истинность одного из них обязательно означает ложность другого, и наоборот – ложность одного обусловливает истинность другого. К противоположным и противоречащим суждениям мы ещё вернёмся, когда речь пойдёт о логических законах противоречия и исключённого третьего.

Рассмотренные отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата (рис. 32), который был разработан ещё средневековыми логиками:

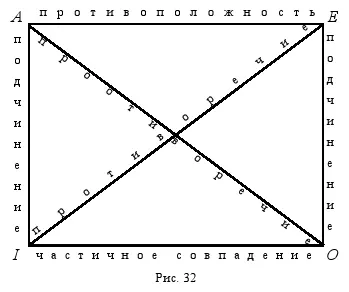
Вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так, суждения вида A и вида I , а также суждения вида E и вида O находятся в отношении подчинения. Суждения вида A и вида E находятся в отношении противоположности, а суждения вида I и вида O – частичного совпадения. Суждения вида A и вида O , а также суждения вида E и вида I находятся в отношении противоречия. Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т. е. равнозначность – это отношение между суждениями A и A , I и I , E и E , O и O . Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения: « Все люди изучали логику », « Некоторые люди не изучали логику ». Видя, что первое суждение является общеутвердительным ( A ), а второе частноотрицательным ( O ), мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Суждения: « Все люди изучали логику (A) », « Некоторые люди изучали логику (I) », находятся в отношении подчинения, а суждения: « Все люди изучали логику (A) », « Все люди не изучали логику (E) », – находятся в отношении противоположности.

Как уже говорилось, важным свойством суждений, в отличие от понятий, является то, что они могут быть истинными или ложными.

Что касается сравнимых суждений, то истинностные значения каждого из них определённым образом связаны с истинностными значениями остальных. Так, если суждение вида A является истинным или ложным, то три других ( I , E , O ), сравнимых с ним суждения (имеющих сходные с ним субъекты и предикаты), в зависимости от этого (от истинности или ложности суждения вида A ) тоже являются истинными или ложными. Например, если суждение вида A : « Все тигры – это хищники », – является истинным, то суждение вида I : « Некоторые тигры – это хищники », – также является истинным (если все тигры – хищники, то и часть из них, т. е. некоторые тигры – это тоже хищники), суждение вида E : « Все тигры – это не хищники », – является ложным, и суждение вида O : « Некоторые тигры – это не хищники », – также является ложным. Таким образом, в данном случае из истинности суждения вида A вытекает истинность суждения вида I и ложность суждений вида E и вида O (разумеется, речь идёт о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).

1. Какие суждения называются сравнимыми и какие – несравнимыми?

2. Что такое совместимые и несовместимые суждения? Приведите по три примера совместимых и несовместимых суждений.

3. В каких отношениях могут быть совместимые суждения? Приведите по два примера для отношений равнозначности, подчинения и частичного совпадения.

4. В каких отношениях могут быть несовместимые суждения?

Приведите по три примера для отношений противоположности и противоречия. Почему противоположные суждения могут быть одновременно ложными, а противоречащие не могут?

5. Что представляет собой логический квадрат? Каким образом он изображает отношения между суждениями? Почему логический квадрат не изображает отношение равнозначности? Как с помощью логического квадрата определять отношение между двумя простыми сравнимыми суждениями?