Карл Саган - Космос

p 2 = 2q 2. (1)

Таким образом, р 2 представляет собой некоторое число, умноженное на 2. Однако квадрат любого нечетного числа является нечетным числом (12 = 1,32 = 9, 52 = 25, 72 = 49 и т. д.). Получается, что само число ρ должно быть четным, то есть можно записать ρ = 2s, где s - некоторое целое число. Подставив его в уравнение (1), находим:

p 2 = (2s )2 = 4s 2 = 2q 2.

Деление обеих частей последнего равенства на 2 дает: g 2 = 2s 2. То есть q 2 тоже является целым числом, и, опираясь на тот же аргумент, что был использован для р , мы заключаем, что q тоже является четным. Но если числа p и q оба делятся на два, значит, они содержат несокращенный общий делитель, что противоречит нашему предположению. Reductio ad absurdum. Но в чем состояло предположение? Доказательство не может запретить нам сократить общие множители, разрешив использовать 14/10, но запретив 7/5. Поэтому ошибочным должно быть начальное предположение: p и q не могут быть целыми числами, a √2 является иррациональным числом. В действительности √2 = 1,4142135...

Насколько ошеломляющее и неожиданное заключение! Какое элегантное доказательство! Но пифагорейцы считали необходимым скрывать это великое открытие.

Правильный многоугольник - это двумерная фигура с определенным числом л одинаковых сторон. В случае л = 3 получается равносторонний треугольник, при η = 4 - квадрат, при л = 5 - правильный пятиугольник и т. д. Многогранник - это трехмерная фигура, все стороны которой являются многоугольниками. Например, куб имеет шесть квадратных граней. Правильным называют многогранник, все грани которого представляют собой одинаковые правильные многоугольники, причем в каждой вершине сходится одинаковое число граней. Для работ пифагорейцев и Кеплера фундаментальное значение имеет факт, что существует пять, и только пять, правильных тел. Простейшее доказательство этого факта можно получить из открытого значительно позже Декартом и Леонардом Эйлером соотношения, связывающего число граней F, число ребер Е и число вершин Ив любом многограннике:

V-E+F=2. (2)

Так, у куба 6 граней ( F= 6) и 8 вершин (V = 8). Отсюда получаем: 8 - Ε + 6 = 2; 14 - Е = 2 и Ε = 12. Уравнение (2) предсказывает, что у куба 12 ребер, и это соответствует действительности. Простое геометрическое доказательство уравнения (2) можно найти в книге Куранта и Роббинса «Что такое математика?» [243] Курант Р., Роббинс Г. Что такое математика? Элементарный очерк идей и методов. РХД, 2001. . Пользуясь уравнением (2), легко доказать, что существует всего пять правильных тел.

Каждое ребро правильного многогранника является общей стороной двух прилегающих друг к другу граней. Возвращаясь к примеру с кубом: каждое ребро - это граница между двумя квадратами. Если мы подсчитаем все стороны всех граней многогранника nF, то каждое ребро окажется сосчитанным дважды, то есть

nF = 2 E (3)

Обозначим r число ребер, которые сходятся в одной вершине. Для куба r = 3. Кроме того, каждое ребро соединяет две вершины. Если мы подсчитаем концы всех ребер /V, то вновь сосчитаем каждую вершину дважды, то есть

rV = 2E (4)

Подставляя выражения для V и F из уравнений (3) и (4) в уравнение (2), получаем:

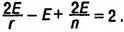
Деление обеих частей уравнения на 2Е дает:

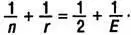
(5)

Мы знаем, что значение л не может быть меньше 3, поскольку треугольник является простейшим многоугольником. Нам также известно, что r не может быть меньше 3, поскольку в каждой вершине многогранника сходится не меньше трех граней. Если n и r одновременно будут больше 3, то с учетом того, что они являются целыми числами, левая часть уравнения (5) окажется меньше либо равна 1/2, и ни при каком значении Е оно не будет превращаться в равенство. Таким образом, осуществив reductio ad absurdum, мы доказали, что либо n =3 и r ≥ 3, либо r = 3 и n ≥ 3.

Если n = 3, уравнение (5) принимает вид

(1/3) + (1/r ) = (1/2) + (1/Е ) или

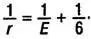
(6)В данном случае г может принимать только значения 3, 4 и 5. (При л, равном и большем 6, уравнение не имеет решений.) Значения n = 3, r = 3 соответствуют многограннику, у которого в каждой вершине сходится по три треугольника. Согласно уравнению (6) он имеет 6 ребер; согласно уравнению (3) у него 4 грани; согласно уравнению (4) - 4 вершины. Очевидно, что это пирамида, или тетраэдр. При n = 3, r = 4 получаем восьмигранник, у которого в каждой вершине сходится по четыре треугольные грани, - октаэдр. Значения n = 3, r = 5 соответствуют икосаэдру - многограннику с двадцатью треугольными гранями, в каждой вершине которого сходится по пять треугольников.

Если r = 3, уравнение (5) приобретает вид

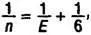
и, повторив аналогичные рассуждения, мы получим, что л может принимать только значения 3, 4 и 5. При n = 3 вновь получается тетраэдр. Значению n = 4 соответствует многогранник, составленный из 6 квадратов, - куб, а при л = 5 результатом будет 12-гранник, состоящий из пятиугольников, - додекаэдр.

Другие сочетания целых чисел не подходят в качестве значений л и л, а значит, существует только 5 правильных многогранников [244] Приведенные рассуждения доказывают лишь то, что правильных многогранников может быть не больше пяти. Из них еще не следует, что хоть один из многогранников, соответствующих допустимым значениям n и r , существует. То, что для всех пар n и r действительно можно построить правильный многогранник, - замечательный факт. Ведь вполне могло бы оказаться, что при каком-нибудь из сочетаний n и r грани не сходятся друг с другом. На этом факте обычно не акцентируют внимание, так как многогранники были известны с глубокой древности и никто не сомневался в их существовании. - Пер. . Этот вывод, полученный в результате красивых абстрактных математических рассуждений, оказал, как вы уже знаете, весьма глубокое воздействие на практические дела людей.

Форзац:Небольшое скопление галактик, включающее в себя крупную спиральную и эллиптическую галактики. Художник А. Шеллер

Заняв наблюдательный пост в межгалактическом пространстве, мы увидели бы россыпь бесчисленных слабых волокон света, напоминающих морскую пену на волнах Космоса. Это галактики. Некоторые из них одинокие странники, но большинство обретается в составе общин – звездных скоплений и, сбившись в кучу, бесконечно дрейфует среди величественной темноты Космоса. Перед нами Космос в самом крупном из известных масштабов. <...> Любая галактика состоит из газа, пыли и звезд – миллиардов и миллиардов звезд. И каждая звезда может быть чьим-то солнцем. Внутри галактики есть звезды, и миры, и, возможно, жизнь, разумные существа, космические цивилизации. Но издали галактики напоминают мне коллекцию любовно подобранных вещиц – ракушек, а может быть, кораллов, творений, над которыми Природа трудилась в космическом океане целые эоны.