Дмитрий Гусев - Удивительная логика

Умозаключения по аналогии(аналогия) (от греч. analogia – «соответствие») – это умозаключения, в которых на основе сходства предметов (объектов) в одних признаках делается вывод об их сходстве и в других признаках. Например:

Планета Земля расположена в Солнечной системе, на ней есть атмосфера, вода и жизнь.

Планета Марс расположена в Солнечной системе, на ней есть атмосфера и вода.

=> Вероятно, на Марсе есть жизнь.

Как видим, сопоставляются два объекта (планета Земля и планета Марс), которые сходны между собой в некоторых существенных, важных признаках (находиться в Солнечной системе, иметь атмосферу и воду). На основе данного сходства делается вывод о том, что, возможно, эти объекты сходны между собой и в других признаках: если на Земле есть жизнь, а Марс во многом похож на Землю, то не исключено наличие жизни и на Марсе. Выводы аналогии, как и выводы индукции, вероятностны.

Все дедуктивные умозаключения называются силлогизмами(от греч. sillogismos – «подсчитывание, подытоживание, выведение следствия»). Существует несколько видов силлогизмов. Первый из них называется простым, или категорическим, потому что все входящие в него суждения (две посылки и вывод) являются простыми, или категорическими. Это уже известные нам суждения видов А, I, Е, О.

Рассмотрим пример простого силлогизма:

Все цветы ( М ) – это растения ( Р ).

Все розы ( S ) – это цветы ( М ).

=> Все розы ( S ) – это растения ( Р ).

Обе посылки и вывод являются в данном силлогизме простыми суждениями, причем и посылки, и вывод – это суждения вида А (общеутвердительные). Обратим внимание на вывод, представленный суждением Все розы – это растения. В этом выводе субъектом выступает термин розы, а предикатом – термин растения. Субъект вывода присутствует во второй посылке силлогизма, а предикат вывода – в первой. Так же в обеих посылках повторяется термин цветы, который, как нетрудно увидеть, является связующим: именно благодаря ему не связанные, разобщенные в посылках термины растения и розы можно связать в выводе. Таким образом, структура силлогизма включает в себя две посылки и один вывод, которые состоят из трех (различным образом расположенных) терминов.

Субъект вывода располагается во второй посылке силлогизма и называется меньшим термином силлогизма(вторая посылка также называется меньшей).

Предикат вывода располагается в первой посылке силлогизма и называется б́ольшим термином силлогизма(первая посылка также называется большей). Предикат вывода, как правило, является по объему большим понятием, чем субъект вывода (в приведенном примере понятия розы и растения находятся в отношении родовидового подчинения), в силу чего предикат вывода называется б́ольшим термином, а субъект вывода – меньшим.

Термин, который повторяется в двух посылках и связывает субъект с предикатом (меньший и больший термины), называется средним термином силлогизмаи обозначается латинской буквой М (от лат. medium – «средний»).

Три термина силлогизма могут быть расположены в нем по-разному. Взаимное расположение терминов друг относительно друга называется фигурой простого силлогизма. Таких фигур четыре, т. е. все возможные варианты взаимного расположения терминов в силлогизме исчерпываются четырьмя комбинациями. Рассмотрим их.

Первая фигура силлогизма– это такое расположение его терминов, при котором первая посылка начинается со среднего термина, а вторая заканчивается средним термином. Например:

Все газы ( М ) – это химические элементы ( Р ).

Гелий ( S ) – это газ ( М ).

=> Гелий ( S ) – это химический элемент ( Р ).

Учитывая, что в первой посылке средний термин связан с предикатом, во второй посылке субъект связан со средним термином, а в выводе субъект связан с предикатом, составим схему расположения и связи терминов в приведенном примере (рис. 34).

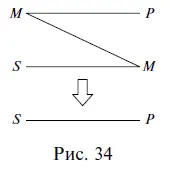
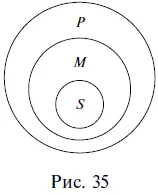
Прямые линии на схеме (за исключением той, которая отделяет посылки от вывода) показывают связь терминов в посылках и в выводе. Поскольку роль среднего термина заключается в том, чтобы связывать больший и меньший термины силлогизма, то на схеме средний термин в первой посылке соединяется линией со средним термином во второй посылке. Схема показывает, каким именно образом средний термин связывает между собой другие термины силлогизма в его первой фигуре. Кроме того, отношения между тремя терминами можно изобразить с помощью кругов Эйлера. В данном случае получится следующая схема (рис. 35).

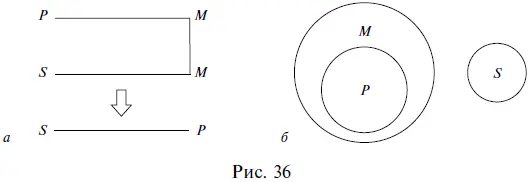
Вторая фигура силлогизма– это такое расположение его терминов, при котором и первая, и вторая посылки заканчиваются средним термином. Например:

Все рыбы ( Р ) дышат жабрами ( М ).

Все киты ( S ) не дышат жабрами ( М ).

=> Все киты ( S ) не рыбы ( Р ).

Схемы взаимного расположения терминов и отношений между ними во второй фигуре силлогизма выглядят так, как показано на рис. 36.

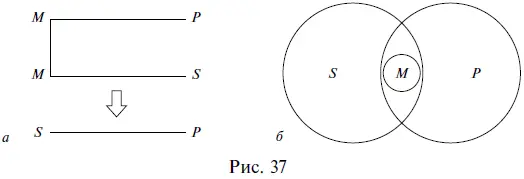
Третья фигура силлогизма– это такое расположение его терминов, при котором и первая, и вторая посылки начинаются со среднего термина. Например:

Все тигры ( М ) – это млекопитающие ( Р ).

Все тигры ( М ) – это хищники ( S ).

=> Некоторые хищники ( S ) – это млекопитающие ( Р ).

Схемы взаимного расположения терминов и отношений между ними в третьей фигуре силлогизма изображены на рис. 37.

Четвертая фигура силлогизма– это такое расположение его терминов, при котором первая посылка заканчивается средним термином, а вторая начинается с него. Например:

Все квадраты ( Р ) – это прямоугольники ( М ).

Все прямоугольники ( М ) – это не треугольники ( S ).

=> Все треугольники ( S ) – это не квадраты ( Р ).

Схемы взаимного расположения терминов и отношений между ними в четвертой фигуре силлогизма показаны на рис. 38.