Джеймс Глейк - Хаос. Создание новой науки

Даже топологу с самой развитой фантазией нелегко представить пространства, обладающее четырьмя, пятью и более измерениями. Однако сложные системы имеют множество независимых переменных, поэтому математикам пришлось смириться с тем, что множество степеней свободы требует фазового пространства, где бесконечно много измерений. Так ничем не ограниченная природа дает о себе знать в бурных струях водопада или в непредсказуемости человеческого мозга. Но кто сумеет справиться с буйным, необоримым чудищем турбулентности, которому присущи многообразие форм, неопределенное число «степеней свободы», бесконечное количество измерений?

Физики имели вполне вескую причину, чтобы с неприязнью относиться к модели, поведение которой столь неясно. Используя нелинейные уравнения, описывающие движения жидкости, мощнейшие суперкомпьютеры мира не могли точно проследить турбулентный поток даже одного кубического сантиметра жидкости в течение нескольких секунд. Конечно, виновата в этом больше природа, нежели Ландау, тем не менее предложенная советским ученым схема производила эффект «поглаживания против шерсти». Даже не имея сколько-нибудь солидных знаний, физик вполне мог заподозрить, что феномен не поддается интерпретации. Подобное ощущение выразил словами великий теоретик квантовой физики Ричард Филлипс Фейнман: «Меня всегда беспокоило, что согласно законам в их современном понимании вычислительной машине нужно выполнить бесчисленное количество логических операций, чтобы выяснилось, что же происходит в пространстве и времени, независимо от того, насколько малым является это пространство и сколь коротким — время. Как подобное может случаться в таком маленьком пространстве? Почему требуется столько усилий, чтобы выяснить наконец, какова дальнейшая судьба отрезка времени или капельки пространства?»

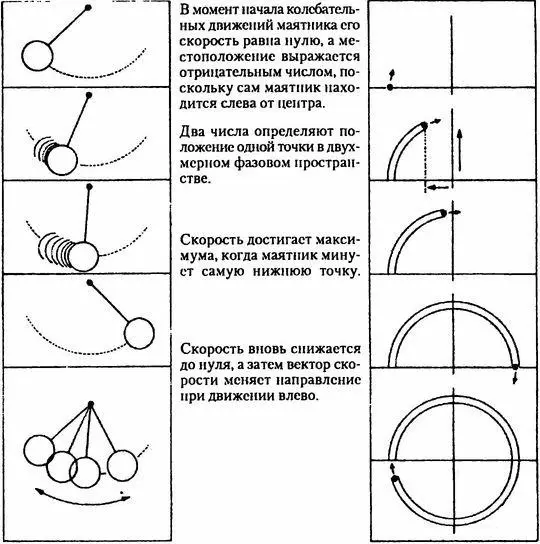
Рис. 5.1. Новый способ изучения маятника.

Одна лишь точка в фазовом пространстве (справа) передает всю информацию о состоянии динамической системы в конкретный момент времени (слева) . Для простого маятника достаточно двух чисел, представляющих его скорость и местоположение.

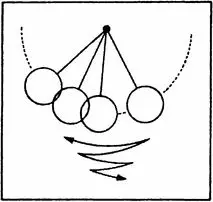
Точки образуют траекторию, которая позволяет наглядно представить непрерывное поведение динамической системы в течение длительного периода времени. Повторяющаяся «петля» отображает систему, которая всегда воспроизводит одно и то же свое состояние. Если повторяющееся поведение устойчиво, как у часов с маятником, система при незначительных помехах возвращается к прежней орбите движения. В фазовом пространстве траектории вблизи орбиты как бы вовлечены в нее, а сама орбита является аттрактором.

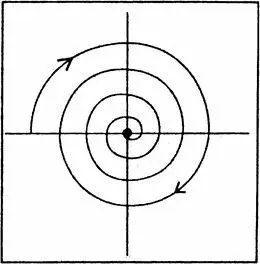
Рис. 5.2. Аттрактор может являть собой одну-единственную точку. В случае с маятником, непрерывно теряющим энергию на трение, все траектории имеют форму спирали, закручивающейся внутрь, по направлению к точке, в которой система устойчива, — в таком случае движения не наблюдается вообще.

Как и многие из тех, кто занимался хаосом, Давид Руэлль подозревал, что видимые в турбулентном потоке объекты: перепутанные струи, спиральные водовороты, волшебные завитки, появляющиеся и вновь исчезающие, — должны отражать то, что объяснялось законами физики, но еще принадлежало к сфере таинственного и неоткрытого. В его понимании рассеивание энергии в турбулентном потоке должно было вести к своеобразному сокращению фазового пространства, притягиванию к аттрактору. Бесспорно, последний не оставался неподвижной точкой, поскольку поток никогда не приходил в состояние покоя, — энергия поступала в систему и уходила из нее. Каким еще мог быть аттрактор? Помимо описанного, согласно догмату, существовал лишь один возможный тип — периодический аттрактор, или замкнутая кривая, орбита, притягивающая все близлежащие орбиты. Если маятник получает энергию от подвеса и теряет ее из-за трения, то устойчивая орбита может представлять собой замкнутую петлю в фазовом пространстве, отражающую, например, регулярные колебательные движения маятника дедушкиных часов. Неважно, где именно начнет двигаться маятник, в конечном счете он придет именно к данной орбите. Но придет ли? В силу неких начальных условий (а они характеризуются минимумом энергии) маятник остановится. Таким образом, получается, что система в действительности имеет два аттрактора, один из которых является замкнутой петлей, а другой — фиксированной точкой. Каждый из аттракторов имеет собственную «нишу» в фазовом пространстве. В целом это напоминает две речные долины, разграниченные водоразделом.

В короткий период времени каждая точка фазового пространства может означать возможное поведение динамической системы. При изучении долгосрочной перспективы единственными моделями поведения становятся сами аттракторы. Все иные типы движения преходящи. По определению, аттракторам присуще важнейшее качество — устойчивость. В реальной системе, где движущиеся элементы сталкиваются и раскачиваются из-за помех окружающей среды, движение обычно возвращается к аттрактору. Толчок способен ненадолго исказить траекторию, однако возникающие случайные движения быстро исчезают, — даже если вдруг кошка заденет часы с маятником, минута не увеличится до шестидесяти двух секунд. Однако турбулентность в жидкостях — явление иного порядка, никогда не порождающее единичный ритм. Известное свойство такого явления заключается в том, что в данный момент времени наблюдается весь спектр возможных колебаний. Турбулентность можно сравнить с «белым шумом» или статикой. Могла ли простая детерминистская система уравнений описывать подобный феномен?

Руэлль и Такенс задались вопросом, обладает ли какой-либо иной тип аттрактора подходящим набором характеристик: устойчивостью, малым числом измерений, непериодичностью. Устойчивость означала достижение конечного состояния системы вопреки всем помехам в полном шумов мире. Малое число измерений предполагало, что орбита в фазовом пространстве должна представлять собой прямоугольник или форму типа коробки, обладающие лишь несколькими степенями свободы. Непериодичность подразумевала отсутствие повторений — ничего общего с монотонным тиканьем старых часов. С геометрической точки зрения вопрос казался чистой воды головоломкой. Какой вид должна иметь орбита, изображаемая в ограниченном пространстве, чтобы она никогда не повторяла и не пересекала саму себя? Ведь система, вернувшаяся в свое прежнее состояние, согласно принятой модели, должна следовать по своему обычному пути. Чтобы воспроизвести каждый ритм, орбита должна являть собой бесконечно длинную линию на ограниченной площади. Другими словами, она должна стать фрактальной.