Виктор Звонников - Контроль качества обучения при аттестации: компетентностный подход

Если результат i -го испытуемого намного выше или ниже среднего балла по обоим тестам, то произведение ( X i – X̅ )( Y i – Y̅ ) будет большим и положительным. Таким образом, при прямой связи значений X i и Y i ( i = 1, 2, …, N ) по тестам X и Y большой и положительной получится сумма всех произведений, т.е.

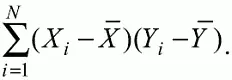
При обратной связи результатов тестирования, когда большинство значений X i выше (ниже) среднего X̅ по тесту X сменяются на значения Y i ниже (выше) среднего Y̅ по тесту Y, сумма

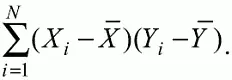
будет меньше нуля и велика по модулю в силу отрицательного знака всех или почти всех произведений ( X i – X̅ )( Y i – Y̅ ) . Наконец, если систематической связи между результатами студентов по тестам X и Y не наблюдается, знак произведения ( X i – X̅ )( Y i – Y̅ ) будет хаотически меняться. Вполне возможно, что для достаточно большой выборки испытуемых, положительные слагаемые будут уравновешиваться отрицательными и потому сумма произведений

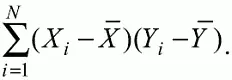
получится близкой к нулю.

Таким образом, произведение ( X i – X̅ )( Y i – Y̅ ) по знаку и абсолютной величине отражает характер связи между наборами данных. Операция усреднения, осуществляемая путем деления суммы произведений отклонений на число испытуемых в выборке, позволяет получить показатель связи, не зависящий от размеров выборок, который называется ковариацией и обозначается символом . Его можно использовать для сравнения мер связи между результатами тестовых измерений по выборкам разного объема.

(6.4)

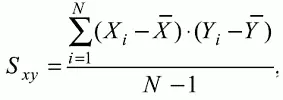
(Замечание, также как и в случае подсчета дисперсии, для различных прикладных задач в статистике удобнее делить не на N, а на N – 1, что при больших размерах выборок не сказывается существенно на величине S xy ) .

Для повышения сопоставимости оценок показателей связи по выборкам с различной дисперсией ковариацию делят на стандартные отклонения. Таким образом, S xy необходимо разделить на S x и S y , где S x и S y – стандартные отклонения по множествам X и Y соответственно. В результате после преобразований получается величина, которая называется коэффициентом корреляции Пирсона r xy :

(6.5)

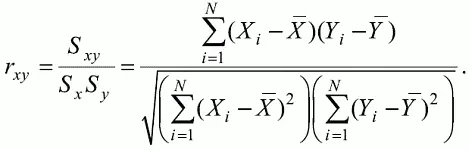
При исследовании связи между наборами данных необходимо правильно выбрать вид и форму показателя, зависящих от шкал, в которых представлены данные (см. подробнее в книге: [7]). В частности, для оценки связи между результатами выполнения учащимися двух заданий теста коэффициент корреляции Пирсона r xy необходимо преобразовать, поскольку результаты выполнения заданий представляются в дихотомической шкале (столбцы из нулей и единиц в матрице данных по тесту). Преобразованный коэффициент Пирсона для дихотомических данных называется коэффициентом ц и вычисляется по формуле

(6.6)

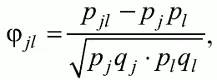
где p jl – доля испытуемых, выполнивших правильно оба задания с номерами j и l , т.е. доля тех, кто получил 1 балл по обоим заданиям; p j – доля испытуемых, правильно выполнивших j -е задание, q j = 1 – p j ; p l – доля испытуемых, правильно выполнивших l -е задание теста, q l = 1 – p l .

Например, для рассматриваемого примера матрицы корреляция между результатами по 5-му и 6-му заданиям теста будет:

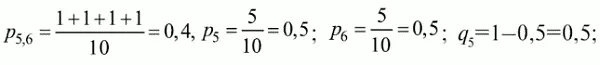
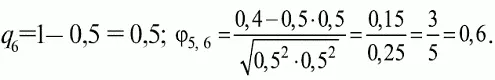
Результаты подсчета значений коэффициента корреляции между всеми заданиями для примера матрицы сведены в табл. 6.4.

Анализ значений коэффициента корреляции в табл. 6.4 позволяет выделить в категорию «плохих» 3-е и 8-е задания теста. Задание 3 отрицательно коррелирует с заданиями 7, 8, 9 и 10. О том, что «виновато» 3-е, а не другие задания теста, свидетельствует анализ значений коэффициента корреляции в столбцах с номерами 7, 9 и 10. В них просматривается только один минус на месте, соответствующем заданию теста 3, которое в свою очередь отрицательно коррелирует с четырьмя заданиями теста. Аналогичная ситуация наблюдается для задания 8. Отрицательные значения коэффициента корреляции указывают на определенный просчет разработчиков в содержании заданий, которые рекомендуется из теста удалить. Наиболее распространенная причина появления отрицательной корреляции – отсутствие предметной чистоты содержания – нередко встречается при разработке самых разных тестов.

Понятно, что предметная чистота – скорее, идеализируемое, чем реальное требование к содержанию любого теста. Например, в тесте по физике всегда встречаются задания с большим количеством математических преобразований, в тесте по биологии – задания, требующие серьезных знаний по химии, в тесте по истории – задания, рассчитанные на выявление культурологических знаний, и т.п. Поэтому можно лишь стремиться к тому, чтобы при выполнении каждого задания доминировали знания по проверяемому предмету.

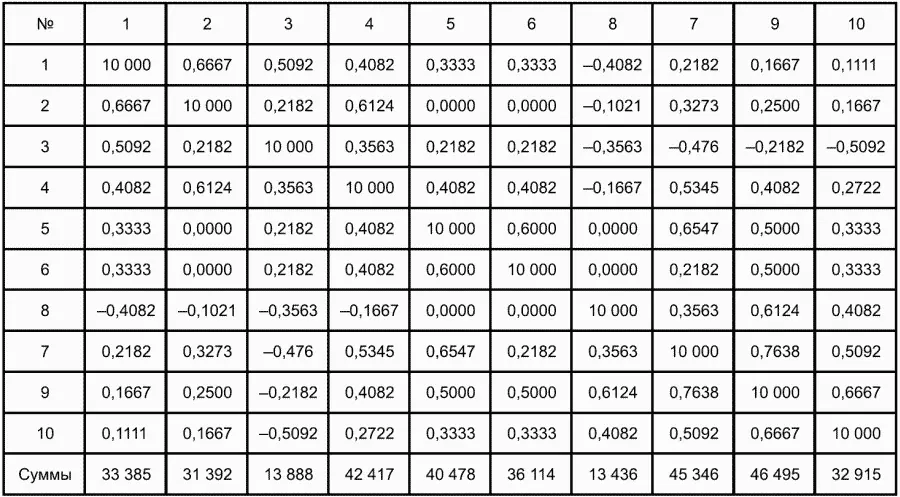
Таблица 6.4 Коэффициенты корреляции заданий

Анализ 9-го столбца табл. 6.4 с максимальной суммой 4,6495, приведенной в конце, указывает на наличие ряда довольно высоких значений коэффициента корреляции (φ 9,8= 0,6124; φ 9,7= 0,7638; φ 9,10= 0,6667), которые могут получить различную трактовку в зависимости от вида разрабатываемого теста. Для тематических тестов высокая корреляция между заданиями неизбежна, так как они в большинстве своем имеют слабо варьирующее исходное содержание, что вполне объяснимо назначением теста. Однако для итоговых тестов высокой корреляции между заданиями по возможности стараются избегать, поскольку вряд ли имеет смысл включать в итоговый тест несколько заданий, оценивающих одинаковые содержательные элементы. Поэтому в итоговых аттестационных тестах обычно стремятся к невысокой положительной корреляции, когда значения коэффициента варьируют в интервале (0; 0,3), и каждое задание привносит свой специфический вклад в общее содержание теста.