Виктор Звонников - Контроль качества обучения при аттестации: компетентностный подход

Далее с помощью подсчета значений точечного бисериального коэффициента корреляции можно оценить валидность отдельных заданий теста. Бисериальный коэффициент корреляции используется в том случае, когда один набор значений распределения задается в дихотомической шкале, а другой – в интервальной. Под эту ситуацию подпадает подсчет корреляции между результатами выполнения каждого задания (дихотомическая шкала) и суммой баллов испытуемых (интервальная или квазиинтервальная шкала) по заданиям теста.

Формула для вычисления значения точечного бисериального коэффициента r pbis, имеет вид:

(6.7)

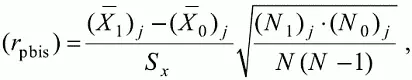
где ( X̅ 1) j — среднее значение индивидуальных баллов испытуемых, выполнивших верно j- е задание теста; ( X̅ 0) – среднее значение индивидуальных баллов испытуемых, выполнивших неверно j -е задание теста; S x — стандартное отклонение по множеству значений индивидуальных баллов; ( N 1) j – число испытуемых, выполнивших верно j-е задание теста; ( N 0) j— число испытуемых, выполнивших неверно j -е задание теста; N — общее число испытуемых, N = N 1+ N 0 .

Применение формулы (6.7) для данных по 5-му заданию рассматриваемого примера матрицы дает достаточно высокое значение точечного бисериального коэффициента.

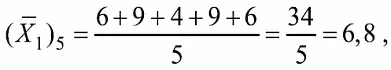
так как 1, 4, 5, 9 и 10-й испытуемые выполнили задание 5 верно.

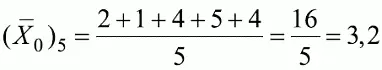
так как 2, 3, 6, 7 и 8-й испытуемые выполнили задание 5 неверно. Стандартное отклонение, подсчитанное для рассматриваемого примера ранее, S x ≈ 2,6; ( N 1) 5 = ( N 0) 5= 5; N = 10. Поэтому

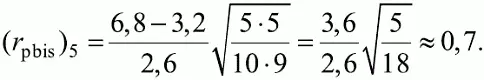
Значения бисериального коэффициента корреляции десяти заданий с суммой баллов по тесту r bis, рассчитанные с помощью компьютерных программ для данных матрицы, приводятся в табл. 6.5

Таблица 6.5 Значения коэффициента бисериальной корреляции

Анализ значений коэффициента бисериальной корреляции в табл. 6.5 указывает на два довольно неудачных задания теста – 3-е [( r bis) 3= 0,26] и 8-е [( r bis) 8= 0,24], которые имеют низкую валидность и должны быть удалены из теста. В целом задание можно считать валидным, когда значение (r bis) j≈ 0,5 или выше этого числа. Оценка валидности задания позволяет судить о том, насколько оно пригодно для работы в соответствии с общей целью создания теста. Если эта цель – дифференциация студентов по уровню подготовки, то валидные задания должны четко отделять хорошо подготовленных от слабо подготовленных испытуемых тестируемой группы.

Решающую роль в оценке валидности задания играет разность ( X̅ 1) j – ( X̅ 0) j , находящаяся в числителе дроби формулы (6.7). Чем выше значение этой разности, тем лучше работает задание на общую цель дифференциации испытуемых. Значения, близкие к нулю, указывают на низкую дифференцирующую способность заданий теста. В том случае, когда в разности доминирует вклад ( X̅ 0), а не ( X̅ 1), задание следует просто удалить из теста. В нем побеждают слабые испытуемые, а сильные выбирают неверный ответ либо пропускают задание при выполнении теста. Таким образом, подлежат удалению все задания, у которых r bis< 0.

Оценка трудности тестовых заданий в классической теории получается по формуле

p j = R j / N

где p j — доля правильных ответов на j -е задание; R j — количество студентов, выполнивших j -е задание верно; N — число студентов в тестируемой группе; j – номер задания теста, j = 1, 2, …, n. Трудность задания нередко выражают в процентах, тогда оценку, полученную по формуле (6.8), умножают на 100%.

Долю правильных ответов на задание p j естественно интерпретировать как легкость задания, в то время как трудность скорее ассоциируется с долей неправильных ответов q j , которая находится путем вычитания p j из единицы: q j = 1 – p j . Однако по сложившейся традиции в классической теории тестов за трудность задания принимается именно доля p j . Для рассматриваемого примера матрицы доля правильных ответов на первое задание p 1= 9/10 = 0,9, а доля неправильных ответов q 1= 1 – 0,9 = 0,1 и т.д. После перевода доли p 1в проценты (0,9 · 100% = 90%) первое задание следует отнести к категории крайне легких: его выполнили 90% тестируемой выборки студентов.

Подбор заданий по трудности в тесте удобно оценить с помощью гистограммы (рис. 6.3).

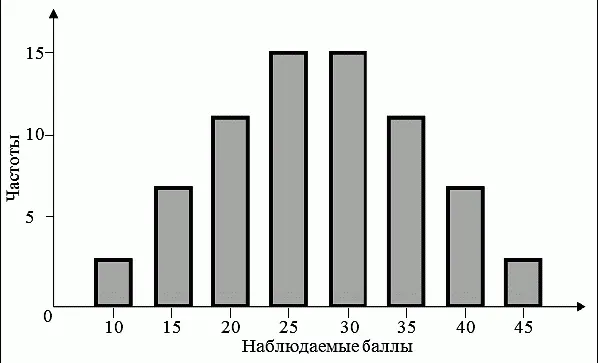
Рис. 6.3. Гистограмма хорошо сбалансированного по трудности нормативно-ориентированного теста

В хорошо сбалансированном по трудности нормативно-ориентированном тесте есть несколько самых легких заданий со значениями p → 0. Есть несколько самых трудных с p → 1. Остальные задания по значениям p занимают промежуточное положение между этими крайними ситуациями и имеют в основном трудность 60–70%. Дополнительный аргумент в пользу преимущественного включения заданий средней трудности с p =̣ 0,5 связан с подсчетом дисперсии по каждому заданию теста, которая для дихотомического набора данных будет равна σ j = p j q j , ( j = 1, 2, …, n ) . Так как произведение p j q j достигает максимального значения (0,5 · 0,5 =̣ 0,25) при p j =̣ 0,5 =̣ q j , то в рамках нормативно-ориентированного подхода наиболее удачными считаются задания средней трудности p = q =̣ 0,5, обеспечивающие максимальный вклад в общую дисперсию теста. В пользу преимущественного выбора заданий средней трудности также говорит подсчет ошибки измерения, которая уменьшается по мере продвижения к центру, где расположены задания средней трудности, и увеличивается на концах распределения.

В критериально-ориентированных тестах основную массу составляют достаточно легкие задания, которые выполняют верно не менее 80–90% испытуемых, чтобы обеспечить достаточно низкий процент не аттестованных студентов, не прошедших по результатам тестирования за критериальный балл.