Лиза Рэндалл - Закрученные пассажи: Проникая в тайны скрытых размерностей пространства.

Рассказчик от автора Э. Квадрат (тезка автора Эдвина А. Эбботта) знакомится с реальностью третьего измерения. На первом этапе своего обучения, когда он все еще привязан к Флатландии, он наблюдает трехмерный шар, проходящий вертикально сквозь его двумерный мир. Так как Э. Квадрат привязан к Флатландии, он видит последовательность дисков, размеры которых сначала увеличиваются, а затем уменьшаются. Эти диски представляют собой срезы шара во время его прохождения через плоскость Э. Квадрата (рис. 6).

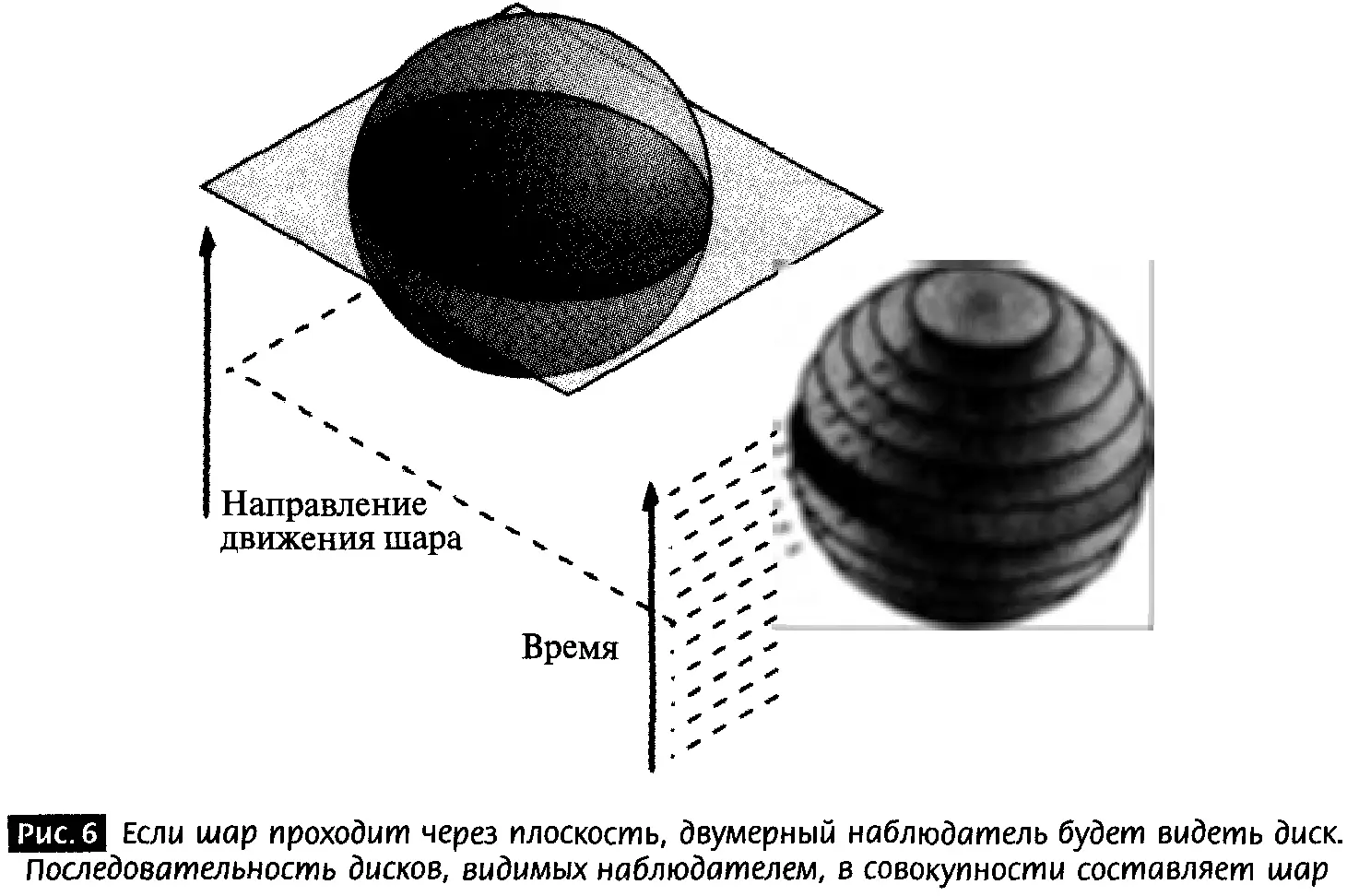
Двумерный наблюдатель, никогда не представлявший себе более двух измерений и никогда не видевший трехмерный объект вроде шара, будет сначала сбит с толку этим зрелищем. Пока Э. Квадрат не сможет подняться из Флатландии в окружающий трехмерный мир, он не сможет по-настоящему вообразить шар. А поднявшись, он постигает шар как образ, созданный склеенными вместе двумерными дисками. Даже в своем двумерном мире, для того чтобы построить шар, Э. Квадрат может начертить видимые им диски как функции времени (см. рис. 6). Но этого не случится до тех пор, пока путешествие сквозь третье измерение не убедит его, что он полностью понимает, что такое шар и его третье пространственное измерение.

По аналогии, мы знаем, что если гиперсфера (шар с четырьмя пространственными измерениями) будет проходить сквозь нашу Вселенную, нам это будет представляться как временная последовательность трехмерных шаров, размеры которых сначала увеличиваются, а затем уменьшаются. К сожалению, у нас нет возможности попутешествовать сквозь дополнительное измерение. Мы никогда не увидим неподвижную гиперсферу во всей полноте. Тем не менее мы можем сделать выводы о том, как эти объекты выглядят в пространствах с разным числом измерений, причем даже тех, которые мы не видим. Мы можем уверенно утверждать, что наше восприятие гиперсферы, движущейся сквозь три измерения, будет похоже на восприятие последовательности трехмерных шаров.

В качестве другого примера вообразим построение гиперкуба — обобщения куба на случай более трех измерений. Линейный отрезок в одном измерении состоит из двух точек, связанных прямой одномерной линией. В случае двух измерений это можно обобщить до квадрата, поместив один из отрезков над другим и соединив их концы двумя дополнительными отрезками. Совершая далее пассаж к кубу в трех измерениях, мы можем построить его, помещая

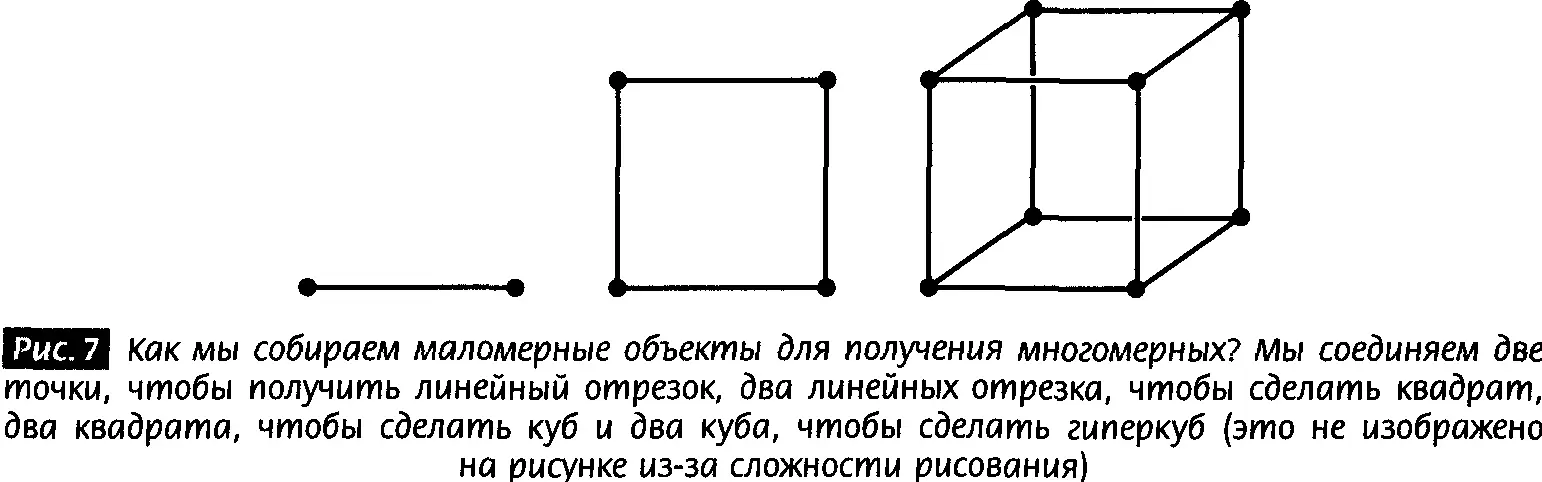
один двумерный квадрат над другим и связывая их четырьмя дополнительными квадратами, по одному на каждую сторону исходных квадратов (см. рис. 7).

В четырех измерениях куб обобщается до гиперкуба, а в пяти измерениях — до чего-то, чему еще нет названия. Но даже если мы, трехмерные существа, никогда не видели эти два объекта, мы можем обобщить процедуру построения, которая сработала при меньшем числе измерений. Чтобы построить гиперкуб (другое название тессеракт), поместим один куб над другим и свяжем их путем добавления шести дополнительных кубов, соединяющих грани двух исходных. Такое построение представляет абстракцию, которую трудно нарисовать, но это ни в коей мере не делает гиперкуб менее реальным.

Когда я училась в средней школе, я провела лето в математическом лагере (что оказалось намного более интересным, чем вы можете подумать), и там нам показали киноверсию «Флатландии » [11] Это мультфильм режиссера Эрика Мартина, сопровождаемый голосами Дадли Мура и других актеров британской комедийной труппы За гранью (Beyond the Fringes). Это было очень смешно. . В конце диктор с очаровательным британским акцентом безуспешно пытается указать на недоступное флатландцам третье измерение, говоря: «Наверх, а не на север!» К сожалению, мы испытаем ту же неудовлетворенность, если попытаемся указать проход к четвертому пространственному измерению. Но точно так же, как флатландцы не видели или не перемещались сквозь третье измерение, хотя оно и существует в истории Эбботта, тот факт, что мы никогда не видели другого измерения, не означает, что его нет. Итак, хотя мы никогда до сих пор не наблюдали такое измерение и не путешествовали сквозь него, лейтмотивом всей книги «Закрученные пассажи » будет фраза: «Не на север, а вперед вдоль пассажа!» Кто знает, что существует из того, чего мы еще не видели?

В оставшейся части этой главы, вместо того чтобы размышлять о пространствах, имеющих более трех измерений, я поговорю о том, как с помощью наших ограниченных зрительных возможностей мы собираемся представлять и рисовать три измерения, используя двумерные образы. Понимание того, как мы совершаем этот пассаж от двумерных образов к трехмерной реальности, пригодится позднее, когда мы будем интерпретировать малоразмерные «картинки» многомерных миров. Относитесь к этому разделу как к разминочному упражнению, для того чтобы приучить ваш мозг к дополнительным измерениям. Было бы неплохо помнить, что в обычной жизни вы все время имеете дело с размерностью. На самом деле все это не так уж незнакомо.

Часто все, что мы можем видеть, — это кусочки поверхностей, которые обрамляют вещи. Хотя эта внешняя оболочка и изгибается в трехмерном пространстве, она имеет два измерения, так как для определения положения любой точки на ней нужно задать два числа. Мы приходим к выводу, что поверхность не трехмерна, так как у нее нет толщины.

Смотря на картины, экраны кинотеатров, мониторы компьютеров или рисунки в этой книге, мы, вообще говоря, смотрим не на трехмерные, а на двумерные изображения. Но тем не менее мы можем восстановить изображенную трехмерную реальность.

Для построения трех измерений мы можем использовать двумерную информацию. Этот процесс включает урезание информации при создании двумерных представлений и одновременно попытку сохранить достаточно информации для воспроизводства важных элементов исходного объекта. Обратимся к часто используемым методам сведения объектов более высокой размерности к меньшему числу измерений: нарезка слоями, проектирование, голография и иногда просто пренебрежение размерностью, — и обратному процессу восстановления тех трехмерных объектов, которые они представляют.

Наименее сложный способ заглянуть за поверхность — сделать тонкие слои. Каждый слой двумерен, но комбинация слоев образует реальный трехмерный объект. Например, когда вы покупаете ветчину в магазине, трехмерный кусок окорока быстро нарезают на много двумерных ломтей [12] Ломти окорока на самом деле имеют некоторую толщину, поэтому они хоть и тонкие, но трехмерные. Их размер в этом дополнительном измерении настолько мал, что в хорошем приближении можно считать ломти двумерными. Однако даже при произвольной толщине двумерных ломтей можно представить себе, как они складываются вместе, образуя трехмерный кусок. . Складывая все ломти, можно реконструировать форму всего трехмерного куска.