Лиза Рэндалл - Закрученные пассажи: Проникая в тайны скрытых размерностей пространства.

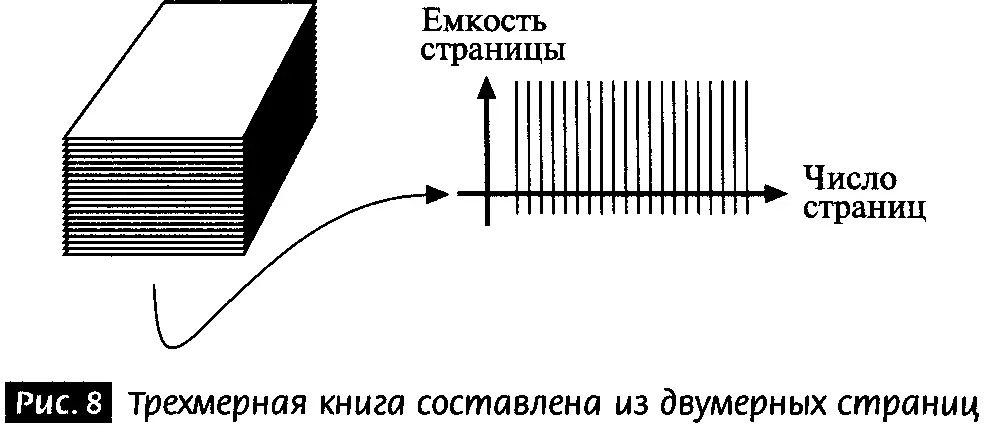
Эта книга трехмерна. Однако ее страницы имеют только два измерения. Объединение двумерных страниц образует книгу [13] Вновь заметим, что для того, чтобы страницы были по-настоящему двумерны, они должны быть бесконечно тонкими, вообще не имеющими никакой толщины в третьем измерении. Однако в данный момент два измерения — это хорошее приближение для страниц такой толщины, как эти. . Можно многими разными способами проиллюстрировать это объединение. Один способ показан на рис. 8, на котором мы смотрим на книгу сбоку. На этом рисунке мы опять играем с размерностью, так как каждая линия представляет страницу. Поскольку все мы знаем, что линии соответствуют двумерным страницам, эта иллюстрация всем ясна. Позднее мы используем аналогичный подход, чтобы изобразить объекты в многомерных мирах.

Разрезание на слои — лишь один из способов заменить высшие измерения более низкими. Другим способом является проектирование — технический термин, заимствованный из геометрии. Проектирование содержит строгие предписания для создания образа объекта, имеющего меньшее число измерений. Тень на стене — один из примеров двумерной проекции трехмерного объекта. На рис. 9 показано, каким образом теряется информация, когда мы (или кролики) осуществляем проектирование. Точки на тени определяются только двумя координатами, лево — право или вверх — вниз на стене. Однако проектируемый объект имеет третье пространственное измерение, которое не сохраняется в проекции.

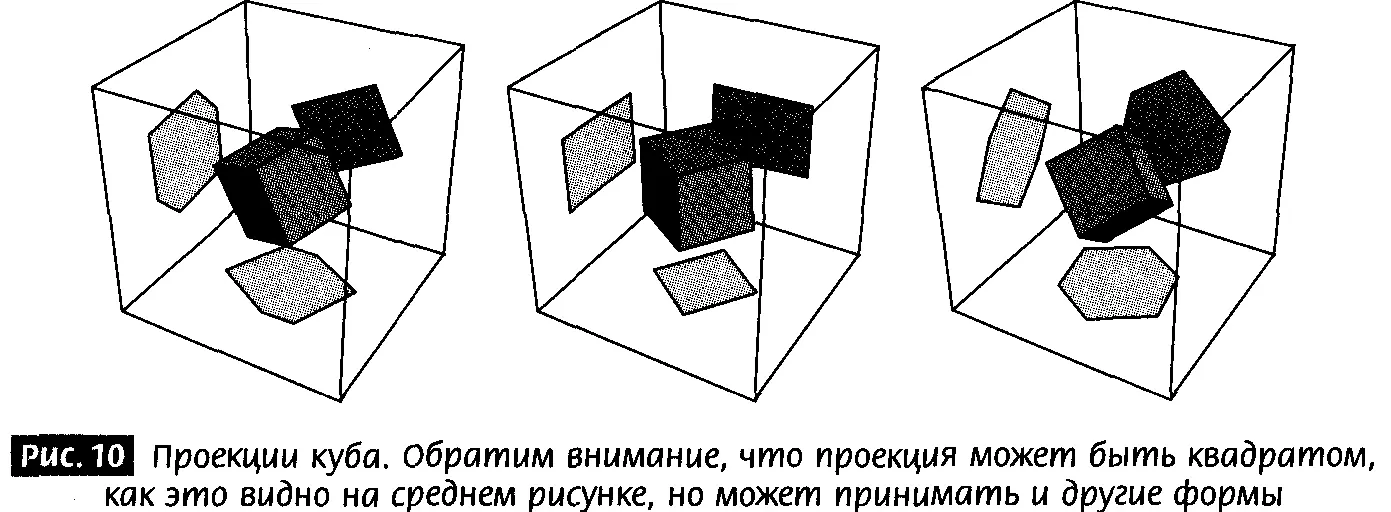
Простейший способ осуществить проектирование состоит в том, чтобы отбросить одно измерение. Например, на рис. 10 показан куб в трех измерениях, спроектированный на два измерения. Проекция куба может иметь много форм, простейшая из которых есть квадрат.

Возвращаясь к предыдущим примерам графиков Икара и Афины, мы можем построить двумерный график Икара, если пренебрежем его вождением спортивных автомобилей. На самом деле нам не важно, сколько сов выращивает Афина, поэтому мы можем построить не пятимерный, а четырехмерный график. Пренебрежение совами Афины и есть проектирование.

Проекция теряет информацию об исходном многомерном объекте (рис. 9). Однако, когда с помощью проектирования мы создаем картину с меньшим числом измерений, мы иногда добавляем информацию, помогающую восстановить часть потерянного. Дополнительной информацией может быть штриховка или цвет, как в живописи или фотографии. Это может быть число, как на топографических картах для указания высоты местности. Наконец, какие-либо метки могут вообще отсутствовать, и в этом случае двумерное описание просто несет меньше информации.

Если бы не оба наших глаза, работающих совместно и позволяющих реконструировать три измерения, все, что мы видим, было бы проекциями. Если закрыть один глаз, восприятие глубины становится грубее. Один глаз создает двумерную проекцию трехмерной реальности. Чтобы воспроизвести три измерения, нужны два глаза.

У меня близорукость на одном глазу и дальнозоркость на другом, поэтому я не могу должным образом объединять изображения от обоих глаз, если не надеваю очков (что случается редко). Хотя мне сказали, что у меня будут проблемы с реконструкцией трех измерений, обычно я этих проблем не замечаю — все вокруг меня выглядит трехмерным. Это происходит потому, что для реконструкции трехмерных образов я полагаюсь на тени и перспективу (и свое знакомство с внешним миром).

Однако однажды в пустынной местности мы с другом пытались дойти до далекого утеса. Мой друг убеждал меня, что мы должны двигаться прямо, а я никак не могла понять, почему он настаивает, чтобы мы шли прямо сквозь скалу. Оказалось, что скала, про которую я думала, что она выступает непосредственно из утеса, полностью загораживая нам путь, находилась на самом деле значительно ближе к нам, перед утесом. Эта скала, которая, как мне казалось, преградит нам путь, на самом деле вообще не имела отношения к утесу. Путаница возникла из-за того, что мы были вблизи утеса около полудня, когда нет никаких теней, и у меня не было способа построить третье измерение, которое бы указало мне, каким образом далекие утесы и скалы расположены относительно друг друга. Я никогда не осознавала своей компенсирующей стратегии с использованием теней и перспективы, до тех пор пока она не дала сбой.

Живопись и черчение всегда требуют, чтобы художники сводили все, что они видят, к спроектированным образам. В средневековом искусстве это делалось максимально простым образом. На рис. 11 показано мозаичное изображение города в виде двумерной проекции. Ничто на этой мозаике не указывает на третье измерение, нет никаких меток или индикаторов его существования.

Со времен Средневековья художники разработали способы делать такие проекции, которые частично исправляют потерю на картине одного измерения. Один подход, противоположный средневековому уплощению пространства, это метод, использованный кубистами в двадцатом веке. Кубистическая картина (например, «Портрет Доры Маар» Пикассо, рис. 12 представляет одновременно несколько проекций, каждая из которых получена под другим углом, и поэтому передает ощущение трехмерности субъекта.

Однако большинство западноевропейских художников со времен Ренессанса для создания иллюзии третьего измерения использовали перспективу и затенение. Одним из важнейших навыков в живописи является способность так свести трехмерный мир к двумерному представлению, чтобы зритель мог обратить процесс и восстановить исходную трехмерную сцену или объект. Наше культурное воспитание приучило нас знать, как расшифровывать образы, даже при отсутствии полной трехмерной информации.

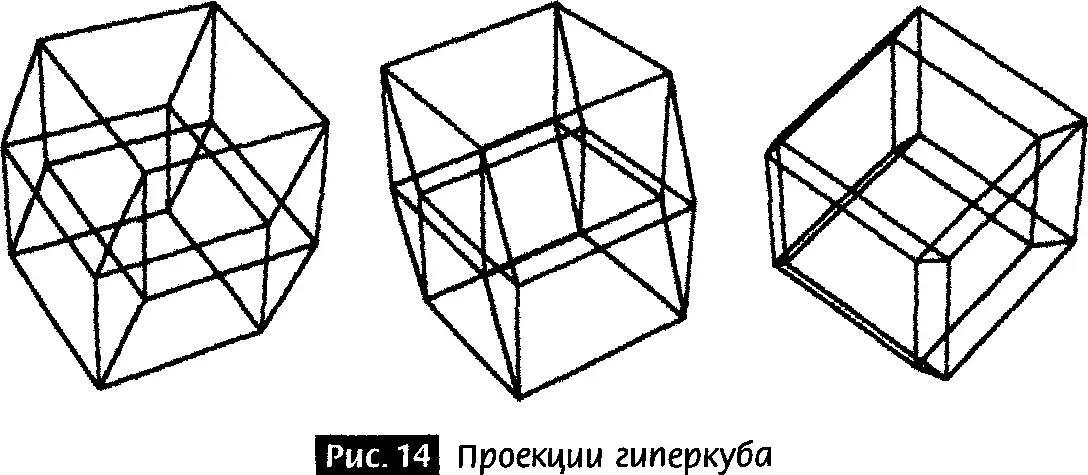
Художники пытались даже представить на двумерных плоскостях многомерные объекты. Например, на картине Сальвадора Дали « Распятие » (Corpus Нуpercubus) (рис. 13) крест показан как развернутый гиперкуб. Этот объект состоит из восьми кубов, прикрепленных друг к другу в четырехмерном пространстве. Именно эти кубы Дали и нарисовал. На рис. 14 я показываю несколько проекций гиперкуба.