С. Капица - Синергетика и прогнозы будущего

Однако, через несколько лет открытие Т-слоя, сделанное, можно сказать, не на кончике пера, а на экране компьютера, было почти одновременно обнаружено несколькими группами экспериментаторов. Использование эффекта Т-слоя позволило создать опытные установки нового типа магнитно-гидродинамических генераторов с заметно большим коэффициентом полезного действия, непосредственно превращающих энергию потока плазмы в электрический ток. Позднее вышли несколько работ соавтора открытия Т-слоя В.С.Соколова с сотрудниками, дающие новые нетрадиционные объяснения природы хромосферных вспышек на Солнце и сопровождающих их явлений через эффект Т-слоя.

Другой пример – возникновение и разработка в работах научной школы академика А.А.Самарского в ИПМ АН СССР и на ВМК МГУ новых парадоксальных представлений синергетики, связанных с изучением явлений, сопровождающих развитие в нелинейной среде режимов с обострением. Любопытно отметить, что физическая и математическая теория режимов с обострением возникла на острие исследований по лазерному термоядерному синтезу.

Весьма небольшая часть работ, иллюстрирующих сказанное и отражающая применение компьютерного моделирования нелинейных процессов, приведена в списке литературы к введению.

Когда слушают на "репетиции" доклад студента или аспиранта, которому предстоит защищать диплом или диссертацию, то часто советуют обо всем упомянуть кратко, а на одном результате остановиться детальнее. Последуем и мы этому традиционному совету. Обсудим несколько подробнее теорию нелинейных сред с положительной обратной связью.

Эта теория весьма велика. Только представителям научной школы, работавшим над этими проблемами в Институте прикладной математики им.М.В.Келдыша РАН, Московском физико-техническом институте и Московском государственном университете принадлежит здесь около 500 работ. Построенная теория активно использовалась при исследовании задач физики плазмы, анализе проектов управляемого термоядерного синтеза, проблем лазерной термохимии и ряда других. Она привела к постановке многих необычных математических задач, решения которых обладают парадоксальными свойствами. Построенная теория послужила основой для интересных философских интерпретаций. Здесь же мы остановимся лишь на нескольких важных идеях и некоторых результатах, существенных для последующего изложения.

Принципиальным понятием в классической механике является материальная точка. Изменение ее состояния определяется вторым законом Ньютона, а само состояние полностью характеризуется шестью числами. Три числа задают координаты точки 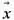и три – ее скорость 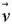. При этом большинство рассматриваемых объектов было таково, что преобразование

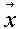
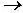
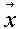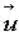+ t,

где 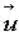некоторая постоянная скорость, не меняет хода процессов в них (математики говорят, что законы механики инвариантны относительно группы преобразований Галилея). При получении многих фундаментальных результатов естествознания, начиная с описания траекторий планет, традиционным предположением было допущение о несущественности диссипативных процессов, связанных с рассеиванием энергии. К ним относятся теплопроводность, трение, вязкость. Эти представления вошли в кровь и плоть современной науки и техники. В особенности, предположение о возможности описать объект с помощью конечного набора чисел (математики называют это гипотезой о конечномерности фазового пространства ). Действительно, трудно представить себе, что, познавая мир, человек вынужден иметь дело с бесконечным набором параметров. Каковы эти числа и откуда они берутся, также на заре классической механики было понято.

Однако уже Лапласом для описания реальности было введено новое фундаментальное понятие – сплошная среда. Это понятие является ключевым при описании процессов, которые развертываются не только во времени, но и в пространстве. При этом приходится считать, что для описания состояния каждой точки нужно знать несколько чисел.

В жидкости, например – пять, характеризующих давление, температуру и три компоненты скорости. Если в вакууме распространяется электромагнитная волна, то нужно 6 чисел, три определяют электрическое поле и три магнитное, и т.д. Объекты такого типа принято называть распределенными в отличие от сосредоточенных , состояние которых характеризует конечный набор чисел. Для описания таких систем Лапласом был предложен новый класс математических моделей – уравнения в частных производных. С помощью этого языка сформулированы выдающиеся достижения нашей цивилизации – уравнения гидродинамики, уравнения Максвелла, уравнение Шредингера.

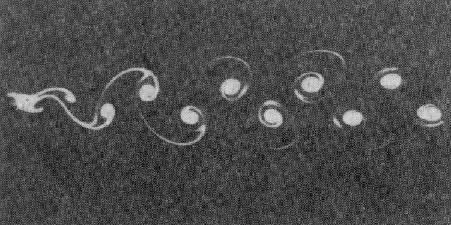
Распределенные системы или сплошные среды являются одним из наиболее сложных и интересных объектов современного естествознания. Представление о сложности процессов, которые могут иметь место в таких системах, дают картины течений жидкости (см. рис.11). Обратим внимание на причудливую геометрию наблюдаемого явления, на спонтанно возникающую упорядоченность, структуры. С более глубоким пониманием пространственно-временных процессов связан ряд высоких технологий и многие фундаментальные научные проблемы. Более глубокое понимание нерегулярных, турбулентных течений жидкости открыло бы дорогу к более быстрым и экономичным кораблям и самолетам. Совершенствование компьютеров и огромного большинства электронных систем неразрывно связано с технологией создания структур на микроуровне. Наконец, переход с молекулярного уровня на клеточный, на котором, вероятно, ждут разгадки многих тайн живого, связан с анализом не только временной, но и пространственной организации в сложной химической машине, каковой является клетка. И это только начало огромного списка. В этом списке есть и проблемы, непосредственно касающиеся будущего человечества. К уравнениям в частных производных, описывающим распределенные системы, относится ряд математических моделей демографии, социологии, экономической географии, науковедения. Их начали применять при описании исторических процессов.

.