С. Капица - Синергетика и прогнозы будущего
- Название:Синергетика и прогнозы будущего
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
С. Капица - Синергетика и прогнозы будущего краткое содержание
С позиций синергетики и нелинейной динамики рассматриваются проблемы, еще недавно целиком относившиеся к сфере гуманитарного знания. Среди них математическое моделирование исторических процессов, глобальные демографические прогнозы, стратегическое планирование будущего человечества, изменение императивов развития цивилизации, прогноз развития системы образования. Актуальность и острота обсуждаемых проблем побудила авторов прибегнуть к необычной форме изложения. Анализ научных результатов в различных частях книги предваряет предельно простое и ясное изложение развиваемых авторами концепций и получаемых выводов. Это делает книгу доступной не только для студентов, аспирантов, исследователей, но и для широкого круга читателей, интересующихся завтрашним днем человечества.
Синергетика и прогнозы будущего - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
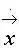 =
= 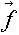 (
( 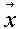 ),
),
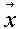 є (x1 , ..., xp )
є (x1 , ..., xp )
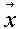 (0) =
(0) = 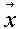 0
0
{a i} = {a 1, ..., a N}, a i=g( 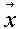 (iDt)
(iDt)
где Dt – заданный интервал времени. Алгоритмы для нахождения функции 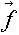 и g, размерности пространства p получили название алгоритмов реконструкции аттракторов . Функция
и g, размерности пространства p получили название алгоритмов реконструкции аттракторов . Функция 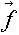 , определяющая дифференциальное уравнение (в дискретном случае можно рассматривать отображение
, определяющая дифференциальное уравнение (в дискретном случае можно рассматривать отображение 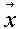 n+1=
n+1= 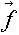 (
( 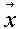 n)) позволяет построить предсказывающую систему или предиктор для исследуемого процесса [16, 17]. Задача (6) о построении динамической системы по временному ряду, вообще говоря, некорректна. Один и тот же ряд можно "объяснить" с помощью различных динамических систем. Поэтому при исследовании (6) используется различная априорная информация и упрощающие предположения. Тем не менее в ряде случаев использование уже существующих алгоритмов решения сформулированной задачи могло бы помочь пленникам пещеры. В частности, они могли бы оценить величину p, отражающую число существенных переменных или размерность фазового пространства, в котором разворачиваются процессы в наблюдаемой ими части реальности.
n)) позволяет построить предсказывающую систему или предиктор для исследуемого процесса [16, 17]. Задача (6) о построении динамической системы по временному ряду, вообще говоря, некорректна. Один и тот же ряд можно "объяснить" с помощью различных динамических систем. Поэтому при исследовании (6) используется различная априорная информация и упрощающие предположения. Тем не менее в ряде случаев использование уже существующих алгоритмов решения сформулированной задачи могло бы помочь пленникам пещеры. В частности, они могли бы оценить величину p, отражающую число существенных переменных или размерность фазового пространства, в котором разворачиваются процессы в наблюдаемой ими части реальности.
По-видимому, часть исторических явлений (в которых ключевыми являются макроэкономические, демографические и другие медленные процессы) допускает удовлетворительное динамическое описание. В то же время другая часть (ряд политических решений, многие военные столкновения и другие) возвращает нас к ситуации "плоскатиков на сфере" и проблемам теории управления.
В соответствии с этим развиваются несколько основных подходов к динамическому прогнозу исторических процессов. В первом, трудности получения "среднесрочного исторического прогноза" (10-20 лет) связывают с тем, что в изучаемой системе имеет место детерминированный хаос. Типичная локальная картина в этом случае представлена на рис.9. Система обладает чувствительностью к начальным данным и бесконечно близкие траектории в ней обычно экспоненциально разбегаются (см. рис.9).
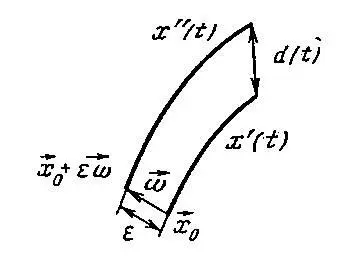
Рис. 9. Устойчивость данной траектории x(t) зависит от поведения бесконечно близких траекторий.
И действительно, А.Ю.Андреевым и М.И.Левандовским была предложена модель, обладающая странным аттрактором [5]. Для описания забастовочного движения эта модель представляет собой модификацию известной в химической кинетике системы Ресслера, которая использовалась также при описании эпидемий. Построенная динамическая система имеет вид
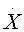 = m (N-X) - bXZ
= m (N-X) - bXZ
 = bXZ - (m+a)Y
= bXZ - (m+a)Y
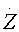 = aY - (m+g) Z
= aY - (m+g) Z
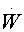 = gZ - mW
= gZ - mW
Здесь N – общее число рабочих, занятых на предприятиях губернии, X – число рабочих, еще не воспринявших информацию о забастовке, Y – рабочие, согласившиеся забастовать, но не ведущие активную агитацию, Z – рабочие, становящиеся агитаторами, W – рабочие, отказавшиеся от участия в стачечной борьбе после одной из забастовок. Оказалось, что эта модель вполне удовлетворительно количественно описывает число рабочих, бастовавших во Владимирской губернии в 1895 – 1905 гг. Любопытно, что одна из базовых моделей нелинейной динамики – система Ресслера, оказалась весьма удобным и универсальным "строительным блоком" для построения математических моделей в нескольких областях.
Другой подход связан с представлением о точках бифуркации исторического процесса. В этой модели считается, что долговременные исторические изменения описываются динамической системой, зависящей от параметра l
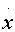 = -
= - 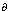 U( x ,l)/
U( x ,l)/ 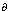 x ,
x ,
Например, таким параметром может быть "историческое время". При изменении параметра в системе (8) может происходить бифуркация. Малые случайные воздействия при этом могут оказаться решающими при выборе ветви бифуркационной диаграммы. В исторической интерпретации это соответствует возрастанию роли отдельных личностей, появлению возможности влиять на ход исторических процессов с помощью малых воздействий. В терминологии нелинейной динамики, выбор ветви связывается с принципом "возникновения порядка через флуктуации" [16, 18]. В принципе, может быть разработана техника, позволяющая диагностировать точки бифуркации. Приведем пример, иллюстрируюший такой подход. В физике известен феномен критических флуктуаций, когда в точке фазового перехода возникают гигантские случайные отклонения, охватывающие всю систему. Аналогичные явления могут иметь место в точках бифуркации исторического процесса. Наглядный пример этого – огромный рост тиража и влияния на общественную жизнь в годы так называемой "перестройки" журнала "Огонек". После перехода к новому общественному укладу этот журнал утратил влияние и стал заурядным изданием. Другие примеры дает анализ процессов выбора путей развития в ходе НЭПа [5].
Во всех этих моделях предполагается, что мы имеем систему с известным фазовым пространством сравнительно небольшой размерности. Тогда оправдано и применение методики реконструкции аттракторов, и построение моделей вида (7) и (8). В этой ситуации различные общества должны оказываться в близких точках фазового пространства. Должны быть "исторические аналоги". Техника поиска таких аналогов имела бы большое значение. Например, сегодня мы не можем сказать, насколько похожа "маленькая победоносная война" с Японией в начале века на "чеченскую войну". Однако этот вопрос поставлен вполне корректно и на нынешнем уровне, вероятно, может быть решен средствами исторического анализа и имитационного моделирования.
Вместе с тем можно ожидать, что ряд исторических процессов требует для своего динамического описания фазового пространства достаточно большой размерности. Типичный пример – острое развитие внутриполитической ситуации, приводящее к военным действиям на внешнеполитической арене, к экспорту своих проблем вовне. Предсказуемы ли такие события? Действовать в соответствии с обрисованным выше подходом нельзя. Алгоритмы реконструкции аттракторов в пространстве большой размерности неэффективны. Феноменологическое описание требует знания многих трудно измеряемых параметров. Кроме того, в мировой истории описано множество событий, где волевые решения и случайности сыграли ключевую роль. Грубо говоря, получить динамический прогноз не удается, а статистический прогноз не нужен. В связи с этим разумно ввести новый класс математических моделей, которые можно условно назвать динамическими системами с джокерами.
Читать дальшеИнтервал:
Закладка:






