Александр Петров - Гравитация От хрустальных сфер до кротовых нор

Ньютон установил, что тело, равномерно движущееся по окружности, фактически движется с ускорением (центростремительным), вызванным постоянной силой, направленной к центру окружности: a цс = ν 2 /R. Третий закон Кеплера устанавливает связь между периодами обращения планет вокруг Солнца и их расстояниями от него. Применяя это соотношение к движению по окружности, Ньютон легко нашёл скорость линейного движения: ν ~ 1 /R 2 . Тогда сила, соответствующая центростремительному ускорению и удерживающая планеты на орбитах (пусть пока круговых), должна иметь вид: F ~ 1 /R 2 , то есть должна быть обратно пропорциональной квадрату расстояния от планеты до Солнца. Тогда Ньютон решил выяснить, не управляет ли одна и та же сила движением Луны на орбите и падением яблока на поверхности Земли.

Интуитивно Ньютон понял, что существенно расстояние от центра Земли, а не от её поверхности, хотя это предположение он сумел доказать значительно позднее. Зная период обращения Луны вокруг Земли, было нетрудно подсчитать с помощью третьего закона Кеплера, что центростремительное ускорение Луны по направлению к Земле, как показано выше a цс ~ 1 /R 2 . Ускорение падения тел вблизи поверхности Земли было хорошо известно из опытов. А поскольку Луна находится в 60 раз дальше от центра Земли, чем яблоко на её поверхности, то ускорение для яблока должно быть в 60 х 60 = 3600 раз больше. Число 60 очень удачно для сравнения в данном случае. Используя законы ускоренного движения, легко подсчитать, что за одну секунду яблоко должно пролетать к центру Земли расстояние, которое Луна проходит только за одну минуту. Проделав расчёты, Ньютон обнаружил, что они согласуются с наблюдениями с точностью ~ 1% и пришёл к твёрдому убеждению, что движением планет, Луны и всех тел, падающих на землю, действительно, управляет одна и та же сила — тяготение.

Успехи Ньютона как физика были бы невозможны, если бы он не разработал необходимый математический аппарат, о чем мы уже говорили, Это фактически была совершенно новая область математики — математический анализ. С его помощью Ньютон показал, что эллиптическая форма орбит обусловлена движением под действием силы, направленной к одному из фокусов эллипса, величина которой обратно пропорциональна квадрату расстояния от него. Однако только в 1685 году с помощью созданного им аппарата математического анализа Ньютон сумел доказать, что гравитационное притяжение Земли можно рассматривать так, как если бы вся её масса была сосредоточена в центре. Этот факт был принципиальным, он позволил Ньютону обосновать использованный ранее способ сравнения ускорений Луны и яблока.

С помощью своих законов механики Ньютон убедительно доказал, что нет деления на тела, которые притягивают, и тела, которые притягиваются. Все тяготеющие тела взаимопритягиваются, то есть законы гравитации имеют универсальный смысл.

Повторим коротко его вывод. У поверхности Земли все тела падают с одинаковым ускорением g независимо от их массы (веса), а сила, действующая на тело на поверхности Земли, пропорциональна его массе (весу), поэтому F = mg. Далее, согласно третьему закону механики, если на тело массой m со стороны другого тела массой M действует некоторая сила, то тело массой m действует на тело массой M точно с такой же, но противоположно направленной силой. Скажем, не только Земля притягивает Луну, но и Луна притягивает Землю. Следовательно, сила взаимного притяжения двух тел должна быть пропорциональна каждой из масс. То, что эта сила обратно пропорциональна квадрату расстояния между телами было уже установлено. Поэтому сила взаимного притяжения двух масс m и M , удалённых на расстояние r друг от друга, определяется выражением:

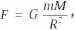
которое и является формулировкой закона всемирного тяготения; здесь G — это коэффициент пропорциональности, называемый постоянной всемирного тяготения. Величина G показывает, насколько сильно гравитационное взаимодействие. Это одна из фундаментальных мировых констант, чисел, значения которых определяют поведение и Вселенной в целом, и отдельных её частей.

Понятие «масса», входящее во второй закон Ньютона, имеет смысл инертной массы — меры сопротивления тела любому изменению состояния его движения. Из второго закона Ньютона следует, что если к двум телам с разными массами приложить одинаковую силу, то менее массивное тело приобретает большее ускорение, чем тело с большей массой. Но понятие «массы» в законе всемирного тяготения имеет другой смысл — это «тяготеющая масса», или мера того, что условно можно назвать «количеством тяготения», присущим данному телу.

Нет логических оснований считать эти два вида массы тождественными. В конце концов, тяготеющую массу можно рассматривать как гравитационный эквивалент электрического заряда; два тела с одинаковой инертной массой могут иметь совершенно различные электрические заряды и, следовательно, приобретать разные ускорения под действием одного и того же электрического поля. В противоположность этому, в гравитационном поле Земли тела как с разными, так и с равными инертными массами всегда падают с одним и тем же ускорением. А это может быть только в том случае, если отношение тяготеющей массы к инертной для всех тел одинаково.

Ньютон провёл серию экспериментов, чтобы выяснить, не оказывается ли это отношение различным для разных тел. Такого различия он не обнаружил, не обнаружено оно и до сих пор. Поскольку эти два вида массы всегда находятся в одной и той же пропорции друг к другу, единицу измерения для них подобрали так, чтобы их отношение оказалось равным единице. Это выражается в том, что формула для силы притяжения на поверхности Земли имеет вид второго закона: F = mg.

Факт равенства инертной и тяготеющей масс известен как принцип эквивалентности. Ниже мы увидим, что этот принцип служит одним из ключевых положений общей теории относительности Эйнштейна.

Значение закона всемирного тяготения нельзя переоценить. Ньютон показал, что тело совершает движение по какой‑либо кривой конического сечения (окружности, эллипсу, параболе или гиперболе) в том случае, если на него действует сила, обратно пропорциональная квадрату расстояния и направленная к фокусу этой кривой. И наоборот, движение тела под действием такой силы подчиняется законам Кеплера. Ньютон показал также, что действием такой универсальной силы можно объяснить движение Луны и планет, ускорение падающих тел, поведение спутников Юпитера и океанские приливы.