Александр Петров - Гравитация От хрустальных сфер до кротовых нор

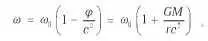
Это означает, что если в данную точку в окрестности тела сигнал пришёл издалека (из бесконечности, где гравитационный потенциал фактически исчезает), то его частота в этой точке станет больше, чем на бесконечности — произойдёт так называемое «фиолетовое» смещение. И наоборот, если пошлём сигнал от тяготеющего тела в область плоского пространства–времени, то там он вое примется с меньшей частотой, то есть его спектр сместится в «красную» область. Уменьшение частоты означает уменьшение энергии сигнала. То есть, покидая тяготеющее тело, электромагнитный сигнал ослабевает, что естественно. На рис. 7.3 отображена следующая ситуация.

Из двух идентичных источников света один расположен на поверхности массивной планеты, другой — далеко, как от неё, так и от всех остальных небесных тел. Наблюдатель находится рядом с последним источником и детектирует свет обоих. Левая картинка соответствует наблюдениям источника на планете, правая — наблюдениям собственного источника. Сравнивая свет от обоих источников, он найдёт, что свет от планеты «покраснел» (поскольку его частота меньше частоты его собственного источника), и часы на планете идут медленнее его часов.

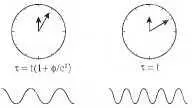
Рис. 7.3. Замедление времени

Также можно сравнить частоту сигнала, если он посылается между двумя точками пространства с разными гравитационными потенциалами. Снова вернёмся к приближению слабого поля для изолированного тела:

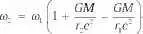
Формула означает, что сигнал, испущенный в точке 1, регистрируется в точке 2. Тогда, например, если точка 2 дальше от центра, чем точка 1, то в ней частота станет меньше. Именно последняя формула лежит в основе третьего эффекта, Если его проверять на Земле, то нужно приёмник разместить выше источника. Из формулы следует, что ожидаемая разность частот в наименьшем приближении будет пропорциональной разности h = r 2 - r 1 по высоте приёмника и источника: Δω/ω = GMh/c 2 , где М — масса Земли. Этот эффект на Земле очень слаб.

В 1925 году гравитационное красное смещение света, испускаемого сверхплотной звездой–компаньоном Сириуса, впервые наблюдал американский астроном Уолтер Адамс (1876–1956). Прямой эксперимент по проверке существования гравитационного красного смещения в поле Земли был осуществлён только в 1960 году сотрудниками Гарвардского университета Робертом Паундом и Гленом Ребкой. Они измеряли сдвиг частоты гамма–излучения, пучок которого направляли вверх и вниз на 23 м по вертикали внутри здания лаборатории. Полученное в этом эксперименте значение красного смещения (относительный сдвиг частоты 2.57·10 –15) совпало с предсказанием теории Эйнштейна с точностью до 1%.

Рассмотренные эффекты обычно называют классическими, предсказанными самим Эйнштейном. Начиная с 60–70–х годов прошлого века, появились новые возможности, с помощью которых проверки ОТО стали значительно точнее. Это радиолокация планет и спутников, а также лазерная локация Луны. После этого четвёртым классическим тестом принято считать задержку радиосигнала в гравитационном поле. Этот эффект был предсказан тоже Эйнштейном, и он тесно связан с отклонением луча света. Отклонение света можно вполне интерпретировать как результат действия линзы — «среды» с другим коэффициентом преломления. То есть гравитирующее тело можно рассматривать как гравитационную линзу ; а поле тела рассматривать как имитатор преломляющей среды. Но эта среда, как мы знаем, не только отклоняет луч света, но и замедляет его: скорость света в среде меньше, чем в вакууме. Точно так же, луч света, проходя рядом с гравитирующим объектом, замедляется по отношению к достаточно удалённому наблюдателю.

Это замедление впервые было обнаружено только в 1964 году Ирвином Шапиро из Массачусетского технологического института (США) в ходе пассивной локации Венеры и Меркурия, находившихся с другой стороны Солнца. Время задержки сигнала, проходящего вблизи Солнца, достигало значения около 240 мкс. Использование этого эффекта оказывается более привлекательным, чем измерение отклонения луча, поскольку интервалы времени могут быть измерены с гораздо более высокой точностью, чем углы, Первые эксперименты с пассивной локацией давали точность 22%. Чтобы измерить временную задержку с наибольшей точностью, необходим космический аппарат, располагающийся за Солнцем При этом сигнал «перерабатывается», чтобы значительно снизить влияние помех, а лишь затем посылается обратно — активная локация. Впервые она было осуществлена группой Шапиро в 1977 году. Точность значительно улучшается при совмещении пассивной и активной локации, когда, например, одновременно с локацией Марса осуществляется локация аппарата рядом с ним. Результат группы итальянских астрофизиков Бруно Бертотти, Лусиано Иесса и Паоло Торторы за 2003 год составляет 1,00001 ∓ 0,000012 от предсказания ОТО, то есть эффект подтверждается с точностью до тысячных процента!

С понятием «гравитационная линза», которое мы ввели выше, связаны бурно развивающиеся в последнее время области исследований в астрофизике и космологии Из российских учёных активными теоретиками-исследователями в этой области являются Михаил Сажин и Александр Захаров. Изложение этой части будет во многом соответствовать статье Захарова «Гравитационные линзы» на сайте pereplet.ru.

По–видимому первый, кто использовал термин «линза» для отклонения луча света гравитационным полем тела, был английский физик Оливер Лодж (1851–1949) в 1919 году. Однако он отметил, что «гравитационное поле действует как линза, но она не имеет фокусной длины». Петербургский физик Орест Хвольсон (1852–1934) в 1924 году опубликовал короткую заметку, в которой заметил, что в случае, когда рассматривается отклонение луча света далёкой звезды звездой–линзой, возможно возникновение второго изображения фоновой звезды, но угол между двумя изображениями столь мал, что эти изображения нельзя разрешить с помощью наземного телескопа. В случае, когда наблюдатель, линза и источник находятся на одной прямой, возникает изображение типа кольца.