Александр Петров - Гравитация От хрустальных сфер до кротовых нор

Объясняется космологическое красное смещение эффектом Доплера. Вспомним, что звук приближающегося поезда выше (частота больше), чем звук удаляющегося.

Аналогично звуковым волнам, такой же эффект имеет место и для электромагнитных волн, в частности, для света: от удаляющегося источника приёмник зарегистрирует свет меньшей частоты (большей длины волны), чем от лабораторного источника, и большей частоты — от приближающегося, Для скоростей значительно меньше скорости света верна формула Доплера: ν = cz. Если сравним её с законом Хаббла, то придём к выводу, что галактики разбегаются и их скорость увеличивается прямо пропорционально расстоянию. Закон Хаббла перепишется в виде:

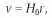
чем дальше от нас галактика, тем больше её скорость.

Величина z также очень удобна для оценки возраста объекта, от которого пришёл свет. Действительно, z прямо связано с расстоянием, а расстояния — значительные и для их преодоления необходимо значительное время. Поэтому сигнал приносит информацию об объекте на более ранних стадиях расширения, Чем больше z, тем более ранняя эпоха исследуется. Отметим, что для больших z простую формулу Доплера необходимо корректировать с учётом ОТО.

Это открытие заставило раз и навсегда отказаться от понятия статичной Вселенной. Кроме того, предсказанное в решениях Фридмана и Леметра, оно стало ещё одним подтверждением правильности новой теории гравитации.

После открытия Хаббла учёные обратили внимание на распределение скоростей, и обнаружили, что оно изотропно, как и полагалось в решениях Фридмана. Это означает, что наблюдатели, помещённые в различные точки пространства, не обнаружат выделенных направлений. Для каждого из них картина распределения скоростей разбегающихся галактик будет выглядеть как для нас: сферически симметричной. Таким образом, предположения Фридмана были сформулированы в виде космологического принципа, согласно которому в больших пространственных масштабах во Вселенной нет выделенных областей и направлений. Большинство специалистов согласно с тем, что любая модель Вселенной должна ему удовлетворять. По современным наблюдательным данным материя во Вселенной распределена однородно и изотропно на масштабах больших 50–100 Мпк.

Существует три типа решений Фридмана. Каждому из них соответствует свой тип геометрии пространства однородной и изотропной Вселенной. Для первого типа — 3–мерное пространство, в котором мы себя ощущаем в каждый момент времени, оказывается бесконечным, безграничным и с отрицательным знаком кривизны. Такие пространства называют гиперболическими, а в решениях Фридмана значение радиуса кривизны увеличивается со временем. Для второго типа решений 3–мерное пространство также оказывается бесконечным и безграничным, но не искривлённым; его называют плоским. Первый и второй типы решений называют открытыми. Для третьего типа решений 3–мерное пространство является безграничным, но не бесконечным — его объём конечен. Это пространство с положительным знаком кривизны; его называют замкнутым. В качестве наглядного примера можно привести 2–мерное пространство обычной сферы. Замкнутое пространство можно классифицировать как 3–мерную сферу, экзотические свойства которой мы обсудим ниже. Примеры 2–мерных поверхностей разного типа приведены на рис. 8.6.

Тип пространства определяется плотностью энергии (или, эквивалентно, массы материи) во Вселенной. Плотность, при которой пространство плоское, называют критической. Если плотность материи меньше критической, то пространство Вселенной будет первого типа, если больше — третьего, Более детальное обсуждение типа космологических решений в зависимости от критической плотности приведено в Дополнении 8.

Поскольку мы уже немного владеем понятием метрики, то здесь будет полезным символически представить метрику решений Фридмана:

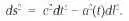
Здесь единственной информативной переменной оказывается величина a(t), которая называется масштабным фактором и показывает, как меняется расстояние между фиксированными частицами в расширяющейся Вселенной. Именно a(t) определяет постоянную Хаббла:

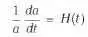
в законе v = Hr. Напомним, что величина H(t ) медленно меняется со временем и постоянна в каждый момент во всем пространстве.

Итак, для метрики Фридмана уравнения ОТО превращаются просто в уравнения для a(t) , плотности р и давления р материи. Связь между плотностью и давлением задаётся уравнением состояния. При решении этих уравнений определяется поведение a(t) в зависимости от времени. Таким образом, увеличение a(t) и означает расширение.

В большой степени на этом уровне для данного типа моделей роль гравитационной теории заканчивается. Далее, в рамках ОТО, самым важным является определение поведения a(t) , что зависит от динамики материи (наполнителя), её взаимопревращений. Дальнейшее изложение будет посвящено именно этому.

Существует различие в характере расширения открытых и замкнутых вселенных Фридмана. В первом случае расширение продолжается, хоть и с замедлением, но бесконечно. На рис. 9.3: кривая I — это гипербола и описывает расширение открытого гиперболического мира, кривая II — это парабола и описывает расширение открытого пространственно плоского мира. В третьем случае расширение в определённый момент сменяется сжатием: кривая III на рис. 9.3 иллюстрирует такое поведение.

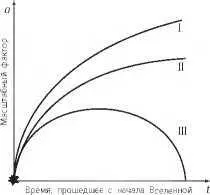
Рис. 9.3. Изменение масштабного фактора

Если представления о бесконечных пространствах обычно не поражают воображение и не требуют пояснений, то таковые необходимы для последнего случая. Свойства 3–мерной сферы напоминают свойства обычной 2–мерной сферы — поверхности шара. Представим путешественника, движущегося по меридиану от Северного полюса к Южному. Миновав Южный полюс, путешественник начнёт возвращаться к Северному, но с другой стороны, Точно так же путешественник в «замкнутом мире» 3–мерной сферы, удаляясь от Земли, достигнет полюса мира на 3–мерной сфере, а затем станет возвращаться к Земле, но с другой стороны.

Но что такое полюс (или противоположная точка по отношению к данной) на поверхности Земли — ясно. А что такое полюс 3–мерной сферы? Вот и начнём объяснения с поверхности Земли, Пусть наблюдатель помещён на Северном полюсе Земли. Пусть радиусами (отрезками меридиана, исходящими из полюса) все большей длины он прочерчивает одну за другой концентрические окружности (данной широты), Эти окружности сначала будут увеличиваться, пока не достигнут максимума на экваторе. Затем, с увеличением радиуса, длины этих окружностей начнут уменьшаться! Наконец, когда длина радиуса достигнет полной длины меридиана, длина окружности превратится в ноль! Мы достигнем Южного полюса — противоположного Северному!