Александр Петров - Гравитация От хрустальных сфер до кротовых нор

Современная физика не может определённо сказать, что происходит на масштабах и в промежутки времени меньше планковских, или при плотностях, давлениях и т. д. — больше планковских. Таким образом, обычно историю развития Вселенной начинают исследовать с некоторого сверхплотного «зародыша», имеющего планковские характеристики. Конечно, вопрос появления самого «зародыша» есть и будет предметом дальнейших исследований.

Например, на основе тех же квантовых представлений при некоторых предположениях предлагаются модели рождения «из ничего». Их основное содержание в том, что Вселенная начинает развиваться из квантовой флуктуации. Важно отметить, что именно модели Фридмана с замкнутым пространством оказываются более подходящими для сценариев квантового рождения Вселенной. Подробнее об этой возможности мы поговорим в главе о гравитационной энергии.

Подведём некоторый итог. Конечно, понятие «Большой взрыв» принципиально отличается от обычных взрывов. Кроме того, это не одномоментное явление, которое происходит в виде разлёта начальной сингулярности, а, скорее, самый ранний период в истории Вселенной, который начинается с планковских масштабов.

Вернёмся к парадоксам не релятивистской космологии. Вспомним, что причина гравитационного парадокса в том, что для однозначного определения гравитационного воздействия либо недостаточно уравнений, либо нет возможности корректно задать граничные условия. В случае фридмановской космологии независимыми являются два уравнения Эйнштейна. Учитывается также уравнение состояния (связи между плотностью и давлением). Кроме того, на данный момент времени из наблюдений известны плотность и скорость расширения,

Все это однозначно определяет эволюцию масштабного фактора a(t) , плотность ρ и давление р. Становится известной геометрия космологического пространства–времени, а значит, тип и динамика 3–мерного пространства, в котором звезды, галактики, скопления галактик ведут себя в соответствии с современными наблюдениями. То есть гравитационного парадокса не возникает.

Теперь зададимся, возможно, провокационным вопросом. А можно ли описать расширяющуюся Вселенную с помощью гравитации Ньютона? Оказывается, можно! Обратимся к опыту Зельдовича. В своих лекциях он всегда старался представить материал простейшим способом, а рассказывая о космологических решениях, по возможности ограничивался теорией Ньютона.

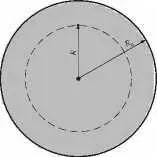
Рис 9.4. Схема расчёта ускорений

Рассмотрим шар радиуса R 0 и элемент массы m внутри шара на расстоянии от центра R < R 0 (рис. 9.4).

Такая задача рассматривалась ещё Ньютоном. Он же и установил, что сила, действующая на m , определяется массой материи внутри сферы радиуса R, а гравитационное действие внешних областей взаимно компенсируется:

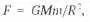
здесь: Μ = (4π/3) R 3ρ — масса материи внутри сферы, ρ — плотность материи, распределённая однородно. Следовательно, ускорение

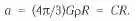
Таким образом, ускорение элемента в точке R пропорционально его расстоянию от центра и не зависит от радиуса шара R 0 при любом, сколь угодно большом R 0 . Это фактически означает, что соотношение справедливо для бесконечной однородной вселенной.

Но остаётся вопрос: решение было найдено для некоторого центра, в котором ускорение равно нулю, а в других точках имеет вполне определённую величину и направлено к центру. А где такой центр в бесконечной однородной вселенной? На самом деле, никакого выделенного центра нет или, если угодно, таким центром может быть любая точка, Возьмём произвольную точку O' находящуюся на некотором расстоянии R O' от «нашего» центра, ускорение которой a O' =-CR O' . Радиус–вектор и ускорение направлены, разумеется, в разные стороны.

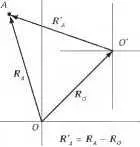
Рис. 9.5. Переход к другой системе координат

Перейдём в систему координат с центром в точке O'

(рис. 9.5). Величины в этой новой системе координат будем обозначать штрихом.

Ускорения в старой и новой системах координат связаны правилом Галилея, которое, если кто забыл, справедливо не только для скоростей, но и для ускорений:

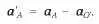
Подставляя в это соотношение выражение для ускорений а А = - CR A и a O' = - CR O' и используя правило сложения векторов R' А = R A - R O' (рис. 9.5), получим:

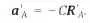
Следовательно, наблюдатель в точке О ' будет видеть ту же картину — все частицы материи имеют ускорение, направленное к нему. Ситуация несколько непривычная — ускорение направлено к центру, но центр «виртуальный», им всегда является точка, в которой находится наблюдатель. Такая ситуация концептуально отличается от ньтоновой, в которой предполагается наличие выделенного пространства, общего для всех наблюдателей.

В приведённом выше расчёте распределения ускорений в однородной вселенной не учитывались начальные скорости. Очевидно, что если начальное состояние статично , т, е. скорости нулевые, то вселенная начнёт сжиматься, плотность и ускорения будут расти.

Рассмотрим ситуацию, когда есть некоторые начальные скорости, направленные от наблюдателя (от «центра»). Для сохранения однородности в постановке задачи необходимо, чтобы начальная скорость была пропорциональна расстоянию от наблюдателя:

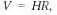
здесь H — коэффициент пропорциональности.

Вселенная будет расширяться, но скорость расширения будет падать. Из‑за расширения будет уменьшаться плотность, а, следовательно, и ускорение. Что «пересилит»? Если начальная плотность достаточно велика, или, если угодно, мала начальная скорость, расширение через некоторое время сменится сжатием. При достаточно большой начальной скорости расширение будет продолжаться вечно. Качественно ситуация аналогична, например, рассмотрению стартовавшей с Земли ракеты. При скорости, большей второй космической, ракета может преодолеть притяжение и улететь на бесконечность.