Александр Петров - Гравитация От хрустальных сфер до кротовых нор

Изложим идею эксперимента Копейкина–Фомалонта. Самым массивным телом в Солнечной системе, которое создаёт переменное гравитационное поле, является Юпитер. Для данного эксперимента его движение можно вполне считать прямолинейным и равномерным. Как на примере этой модели можно представить, что гравитационное взаимодействие передаётся с конечной скоростью? Если бы использовалась теория Ньютона, где скорость передачи гравитационного взаимодействия бесконечна, то эквипотенциальные («равно–силовые») поверхности, перемещались бы, как вмороженные, вместе с Юпитером, оставляя его в центре. Но поскольку скорость распространения конечна, то эквипотенциальные поверхности будут запаздывать. Механизм запаздывания показан на рис. 10.6. Пусть за время Δ t информация о положении

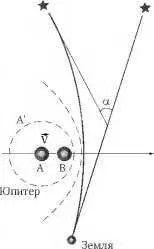
Рис. 10.6. Отклонение радиоволны в переменном поле Юпитера

Юпитера в точке А переместилась до поверхности А'.

Но за это же время Юпитер перейдёт из точки А в точку В, то есть сместится из центра этой поверхности, и т. д.

Теперь ясно, что для оценки скорости гравитационного взаимодействия, нужно оценить степень запаздывания. А для этого необходимо «поэкспериментировать» с переменным гравитационным полем Юпитера, анализируя излучение, проходящее рядом с ним. В качестве источника излучения был выбран радио квазар за Юпитером, радиоволны от которого детектировались на Земле. Наблюдалось положение на небе квазара K' во время прохождения Юпитера и сравнивалось с его же положением К на «чистом» небе. Таким образом определялся угол а отклонения радиоволн переменным гравитационным полем Юпитера.

Теперь предположим, что фундаментальная скорость, которая входит в ОТО — это не с, а независимая скорость распространения гравитационного взаимодействия c g. Какая бы скорость не использовалась, ОТО позволяет рассчитать теоретически переменное гравитационное поле движущегося Юпитера. Электромагнитная волна (фотоны), испущенные квазаром, движутся по геодезическим этого поля. Для определения геодезической существенными являются производные от метрики, которые для переменного гравитационного поля Юпитера характеризуются отношением V /c g , где V — скорость Юпитера. При анализе отклонения радиоволн от квазара рассматривались эффекты, связанные как раз с этим отношением. В пределах точности данного эксперимента было установлено, что скорость распространения гравитационного взаимодействия численно равна скорости света в вакууме, c g= c .

Провести аналогичный эксперимент в поле Солнца невозможно, поскольку оно статично, и уравнение его движения не содержит членов типа V /c g. Вспомним также о гравитационных волнах. В эксперименте Копейкина–Фомалоита речь шла о фундаментальной скорости в ОТО, как скорости передачи гравитационного взаимодействия c g, как бы не связанной с распространением волн. Однако уравнения ОТО устроены так, что гравитационные волны будут распространяться с той же скоростью. После эксперимента можно утверждать, что в пределах точности измерений эта скорость равна с .

Идея сохранения появилась ещё в Древней Греции в виде догадки о наличии неизменных субстанций в мире, где все меняется, Древние материалисты пришли к выводу, что материя как неуничтожима, так и нетворима, и является основой всего существующего мира Одновременно, наблюдение изменений в природе приводит к представлению о вечном движении материи как важнейшем её свойстве.

Эти выводы, скорее, философские. Однако были открыты и конкретные их проявления. Например, ещё Архимеду было известно, что произведение силы, поднимающей груз, на длину рычага — величина постоянная, Значительно позднее, с развитием экспериментальной физики, была сформулирована в виде закона сохранения массы идея о неуничтожимости материи. Его независимо установили основоположник российской естественнонаучной школы Михаил Ломоносов (1711–1765) и французский химик Антуан Лавуазье (1743–1794), систематически применявший в химических исследованиях количественные методы.

Теперь обсудим простые и поучительные опыты Галилея. Исследуя падение тел по наклонной плоскости, он обнаружил, что скорость, которую имеет тело у основания наклонной плоскости, не зависит от угла её наклона, следовательно, от длины пути, а зависит лишь от высоты, с которой падает тело. Это не могло не заинтересовать Галилея, и он продолжил исследовать проблему «наоборот». Для этого он придумал маятник, получивший его имя (рис 11.1). На плоской вертикальной доске, на нити подвешивался груз — это маятник. Если груз отвести в сторону, чтобы он был на высоте h по отношению к низшей точке и отпустить, то он, пройдя низшую точку, поднимался на ту же высоту с другой стороны.

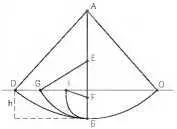
Рис. 11.1. Маятник Галилея

Получается, что скорость в нижней точке тратится на то, чтобы снова подняться выше. А изменится ли эта высота, если изменить траекторию подъёма? Для этого по вертикали, на пути нити, Галилей стал вбивать гвоздики на разном уровне. Тогда траектория подъёма стала разной в разных случаях, как на рисунке. Однако высота груза осталась прежней — h.

Следующим исследователем, значительно продвинувшимся к открытию закона сохранения механической энергии, был нидерландский механик, физик, математик, астроном и изобретатель Христиан Гюйгенс (1629–1695). Он поставил задачу исследовать законы механического движения системы тел. Изучая колебания сложных маятников, он пришёл к выводу, что если система тел приведена в движение силами тяготения, то их общий центр тяжести не может подняться выше того уровня, на котором он находился в начале движения. Заметьте — это обобщение результатов опыта Галилея!

Это вдохновило и других учёных. Лейбниц обратил внимание на то, что из законов свободного падения следует пропорциональность высоты, на которую поднимается колеблющееся тело, квадрату его скорости. Поскольку при колебании без трения высота, с которой падает тело, равна высоте поднятия, то, следовательно, сохраняется произведение mν 2. В современной терминологии — это удвоенная кинетическая энергия. Лейбниц назвал это произведение «живой силой» и предложил идею, что Вселенная обладает сохраняющимся запасом «живых сил». Сохранение «живой силы» было установлено в опытах Гюйгенса с соударением шаров, где при ударе двух тел сумма произведений их масс на квадраты скоростей одинакова до и после удара.