Давид Ласерна - Эйнштейн. Теория относительности. Пространство – это вопрос времени.

Несмотря на то что убеждение Эйнштейна происходило из глубокого, почти инстинктивного понимания феномена электромагнетизма, усвоенного еще в детстве, во время игр на семейной фабрике, ученый понял, что следствия из преобразований Лоренца имели значение не только в рамках электродинамики. Эйнштейн не поддерживал тех, кто изо всех сил пытался разоблачить «заговор Природы», мешавший поискам эфира. Он был более амбициозен и искал единую понятийную парадигму, которая, как законы термодинамики, могла бы объять всю физику. Возможно, почерпнув вдохновение в евклидовых «Началах», ученый стремился сформулировать ряд постулатов, из которых потом с помощью дедукции можно было бы вывести логические заключения. Так, смелые наблюдения, высказанные в объемной статье «К электродинамике движущихся тел», были основаны всего лишь на двух пунктах:

– законы физики принимают один и тот же вид во всех системах отсчета, где движение является равномерным;

– скорость света в вакууме одна и та же для любой инерциальной системы отсчета.

Именно этот подход к науке, разворачивавший целый мир из двусоставного ядра теории, поразил многих читателей статьи. «Метод рассуждения Эйнштейна был для меня настоящим откровением,- признавался Макс Борн, один из отцов-основателей квантовой механики. – Он повлиял на меня сильнее, чем какой-либо другой научный опыт». Постулаты Эйнштейна, в отличие от евклидовых, не были очевидными, как, к примеру, определение точки или прямой. Ученый исходил из экспериментальных данных: «Теория обладает большим преимуществом, если ее главные понятия и основные гипотезы недалеко уходят от опыта».

Второй постулат вступает в противоречие с известной поговоркой о том, что «все относительно». Как заметил Макс Планк, «теория относительности приписывает абсолютный смысл такой величине, которая в классической физике обладает лишь относительным характером, – скорости света». Постоянство скорости света выводится непосредственно из уравнений Максвелла.

Сам Эйнштейн обращал внимание на то, что первый постулат теории «также выполняется в механике Галилея и Ньютона». Все меняла константа скорости света в сочетании с принципом относительности. В довершение всего, к преобразованиям Лоренца можно было прийти исходя непосредственно из второго постулата, безо всяких отсылок к уравнениям Максвелла, что Эйнштейн и проделал в своей статье 1905 года.

Чтобы подтвердить наличие искажения, вызываемого постоянной скоростью света, вернемся на причал к Галилею. Проведем серию экспериментов: сначала – с опорой на законы Ньютона (механическая версия), а потом – на законы Максвелла (электромагнитная версия). Результаты помогут нам совершить теоретическое путешествие, после которого наша картина мира станет гораздо более точной, чем та, которую нам предлагает наш здравый смысл, – а потому гораздо более интригующей и необычной.

Мы уже видели, как преобразования Лоренца вводят новые правила игры, при которых наблюдатели при движении уже не совпадают в своем описании происходящего. Проанализируем, как постоянство скорости света влияет на одновременность двух событий.

У нас есть две системы отсчета, G (оси координат х и y) и D (оси координат х' и y'). Эти системы находятся в мире, где время течет одинаково во всех точках пространства, и потому часы наблюдателей идут с одинаковой скоростью.

Версия наблюдателей, находящихся в корабельном трюме

Два человека, назовем их А' и В' располагаются по углам трюма, смотря в направлении положительного луча оси y'. В центре находится механизм, выбрасывающий одновременно два мяча, один направо, другой налево; оба мяча летят с одинаковой скоростью v. Мы не будем учитывать ни силу тяготения, ни трение.

Третий человек, С' занимает свое место между А' и В' напротив аппарата. А', В' и С' синхронизируют свои часы, и все получают задание зарегистрировать некоторое событие, причем для каждого оно свое. Первый отметит время удара мяча о стену слева, второй – удар мяча о стену справа, а третий (С') – момент, когда машина выбросит мячи (рисунок 3). Когда машина выбрасывает мячи, С' отмечает по своим часам время t' 0(рисунок 4). Когда А' и В' видят, что мяч ударился о соответствующую стену, они отмечают время t' 1и t' 2(рисунок 5).

Оба мяча преодолевают одно и то же расстояние (L'/2) с одной и той же скоростью. Если все три наблюдателя сравнят свои замеры и разности t' 2– t' 0и t' 1– t' 0, они получат одинаковый результат. Заключение: мячи достигли стен в один и тот же момент времени.

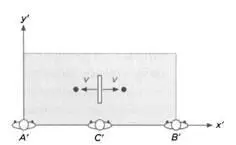
РИС.3

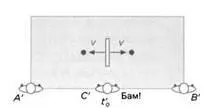
РИС. 4

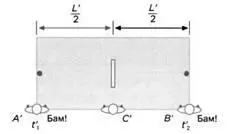
РИС. 5

Версия наблюдателей на причале

Для того чтобы воспроизвести эксперимент, который только что был проведен в трюме, прибегнем к несколько искусственному приему, который, однако, будет полностью ясен при разборе второй, относительной, версии этого опыта. Мы расположим вдоль причала ряд наблюдателей с секундомерами, и каждый будет фиксировать момент события, происходящего точно напротив него (рисунок 6).

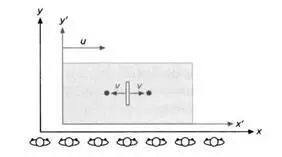
РИС. 6

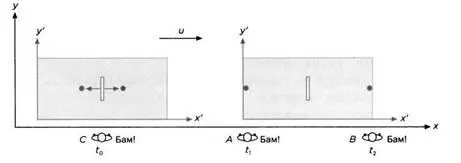
РИС. 7

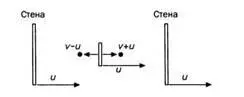
РИС. 8

Корабль движется вдоль причала со скоростью u. Пусть С – наблюдатель, находящийся напротив механизма в момент, когда тот выбрасывает мячи. Время, отмеченное им, будет t 0. А и В – это наблюдатели, фиксирующие момент удара мячей о стены. Они отметят моменты времени t 1и t 2(рисунок 7).

Движение корабля нарушает симметрию между расстояниями, которые пролетает левый мяч (i) и правый мяч (d). До момента выстрела наблюдатели видят, что выстреливающая машина двигается со скоростью и направо. В определенный момент механизм выстреливает мячи в противоположные стороны, оба двигаются со скоростью u. Наблюдатели на причале видят, что мяч i двигается налево со скоростью v – и, а мяч d двигается направо со скоростью v – u. С их точки зрения мяч i летит медленнее, a d – быстрее. Для наблюдателей А' и В' они летели одинаково быстро. Повлияет ли эта разница скоростей на время, за которое каждый из мячей долетит до стены? Нет, потому что левая стена будет двигаться навстречу мячу i со скоростью v, а правая будет с той же скоростью отдаляться от мяча d (рисунок 8).