Давид Ласерна - Эйнштейн. Теория относительности. Пространство – это вопрос времени.

Эти эффекты компенсируют друг друга: медленно летящий мяч преодолевает более короткое расстояние, а быстрый – более длинное. В результате оба долетают каждый до своей стены одновременно. Если наблюдатели A, В и С соберутся вместе и сравнят свои замеры времени, получится, что разности t 2– t 0и t 1– t 0равны между собой. События происходят одновременно.

Заменим метательную машину и мячи фонарем с двумя лампочками. При включении он посылает два световых луча (электромагнитное излучение): один направо, другой налево.

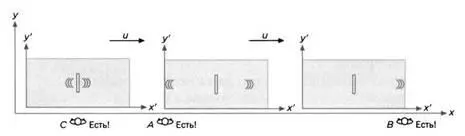
РИС. 9

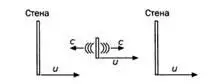
РИС. 10

Версия наблюдателей, находящихся в корабельном трюме

По сути, эксперимент очень похож на предыдущий, как и его результат: мы снова получаем равенство t' 2– t' 0= t' 1– t' 0.

Версия наблюдателей на причале

В предыдущем случае, как мы помним, из-за движения корабля мячи двигались по-разному, но в этом случае константа скорости света не позволит возникнуть эффекту компенсации. Наблюдатели, находящиеся на причале, придут к выводу, что лучи света i и d одинаково быстры (рисунок 9). Но стены по-прежнему будут вести себя по-разному: одна будет приближаться к лучу i, а другая – отдаляться от луча d. Поэтому луч i придет к цели раньше, чем луч d (рисунок 10). События встречи луча света со стеной в системе отсчета G не одновременны!

Продолжим изучать следствия того факта, что скорость света постоянна, в рамках интересующего нас принципа относительности. Допустим, что два наблюдателя, G и D присутствуют при одних и тех же событиях, но видят их с разных точек. Мы попросим их сделать один дистанционный замер.

Два наблюдателя, А’ и В’, располагаются в углах корабельного трюма, глядя в направлении положительного луча оси у' На левой стене закреплен автоматический метатель, который выстреливает мяч со скоростью v. Физический феномен (в этом случае механический), который мы здесь рассмотрим, заключается в метании и остановке мяча, и этим методом мы воспользуемся для того, чтобы измерить трюм корабля. Его длина будет равна дистанции, которую пролетит мяч с момента выстрела до момента своей остановки о противоположную (правую) стену трюма.

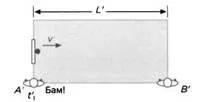
РИС. 11

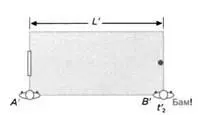
РИС. 12

Версия наблюдателей, находящихся в корабельном трюме

А’ и В’ считают, что находятся в состоянии покоя. А’ засекает на своем хронометре время выстрела мяча (t’1) (рисунок 11). Когда мяч ударяется о стену, В’ отмечает момент времени на своем секундомере (t' 2) (рисунок 12).

Зная скорость v и время t' и t' 1в системе отсчета D можно сделать вывод о расстоянии, пройденном мячом, умножив скорость на период времени. В этом случае:

L'=v•(t' 2-t' 1).

Версия наблюдателей на причале

Нам снова понадобится целый ряд наблюдателей, стоящих вдоль причала, – каждый с хронометром. Пусть А – наблюдатель, который находится напротив метательной машины в момент выстрела. Он отметит на своем хронометре момент вылета мяча из машины (t 1) (рисунок 13). В – тот, кто будет находиться напротив мяча, когда тот ударится о стену. В момент удара он отметит время t 2(рисунок 14).

РИС. 13

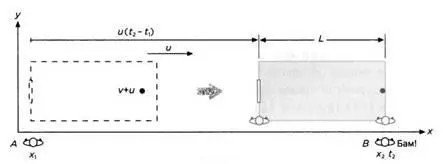
РИС. 14

Наблюдатели считают, что скорость мяча внутри метательной машины уже равна скорости движения корабля и. После выстрела правая стена смещается, отдаляясь от мяча со скоростью u потому мяч должен пройти большую дистанцию. Поэтому несмотря на то, что наблюдатели системы G отметят то же время, что и наблюдатели системы D пройденное расстояние и скорость мяча для них будут разными:

L+u•(t 2-t 1) где u•(t 2-t 1) расстояние, на которое отодвигается правая стена в то время, пока мяч находится в воздухе.

Если мы отвлечемся от существования корабля и будем заниматься только мячом, то увидим, что со скоростью v + u он за период времени t 2– t 1пролетит расстояние

(v + u)•(t 2- t 1).

Обе величины должны быть равны между собой:

L + u • (t 2– t 1) = (v + u) • (t 2– t 1).

Получим знакомое уравнение для вычисления длины трюма:

L = v•(t 2- t 1).

Можно сделать вывод о том, что с точки зрения наблюдателей на причале мяч должен пройти большее расстояние, поскольку стена от него отдаляется, но при этом он летит с большей скоростью, так как к его скорости прибавляется скорость корабля, поэтому оба эффекта компенсируют друг друга.

Заменим метательную машину фонарем, а мяч – лучом света (и опять мы имеем дело с электромагнитным излучением).

Единственный элемент, общий для систем G и D – величина скорости света. Все хронометры, участвующие в эксперименте, произведены на одной фабрике, но только два из них в одной и той же системе отсчета показывают одно и то же время. Для того чтобы перевести пространственные или временные координаты из одной системы в другую, необходимо прибегнуть к преобразованиям Лоренца.

Версия наблюдателей находящихся в трюме корабля

Как и в механическом эксперименте, А’ отмечает тот момент, когда световой луч выходит из фонаря, а В’ – момент, когда луч достигает противоположной стены (рисунок 15). Для них:

L’ = c-(t' 2-t' 1).

Версия наблюдателей на причале

С причала наблюдатели видят, как отдаляется правая стена, световой луч при этом по-прежнему движется со скоростью с (рисунок 16). Они замечают, что прежде чем достичь стены, луч преодолел не только длину трюма, но и дистанцию, пройденную кораблем в период времени между t 1и t 2(рисунок 17):

L +u-(t 2-t 1).

С другой стороны, если оставить корабль в стороне, за временной интервал (t 2– t 1) свет проходит расстояние:

c•(t 2-t 1)=x2 -x1

Приравняв выражения друг к другу:

L + u • (t 2- t 1) = с • (t 2- t 1)=х2- х1

и применив формулу преобразований Лоренца, мы получаем поразительный результат:

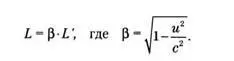
Поскольку скорость корабля меньше скорости света (u < с), то фактор бета меньше t, а значение L меньше, чем L'. То есть для наблюдателей в системе G трюм корабля в длину меньше, чем для наблюдателей в системе D. Это и есть так называемое Лоренцево сжатие.