Antonio Duran Guardeno - Ньютон. Закон всемирного тяготения. Самая притягательная сила природы.
- Название:Ньютон. Закон всемирного тяготения. Самая притягательная сила природы.
- Автор:
- Жанр:
- Издательство:Де Агостини
- Год:2015
- ISBN:2409-0069
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Antonio Duran Guardeno - Ньютон. Закон всемирного тяготения. Самая притягательная сила природы. краткое содержание
Исаак Ньютон возглавил научную революцию, которая в XVII веке охватила западный мир. Ее высшей точкой стала публикация в 1687 году «Математических начал натуральной философии». В этом труде Ньютон показал нам мир, управляемый тремя законами, которые отвечают за движение, и повсеместно действующей силой притяжения. Чтобы составить полное представление об этом уникальном ученом, к перечисленным фундаментальным открытиям необходимо добавить изобретение дифференциального и интегрального исчислений, а также формулировку основных законов оптики. Ньютон, которого многие считают воплощением рациональности, на самом деле был человеком сложным; он много раз вступал в яростные споры со знаменитыми современниками, такими как Лейбниц или Гук, и с не меньшим рвением занимался наукой, алхимией и теологией.
Прим. OCR: Обозначение sqrt() - используется в тексте для замены отсутствующего в наборе знака "корень квадратный".
Ньютон. Закон всемирного тяготения. Самая притягательная сила природы. - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Рассмотрим две функции: с одной стороны – функция s, которая в каждый отрезок времени t определяет расстояние s(t), проходимое телом; с другой – функция v, которая в каждое мгновение времени t определяет скорость v(t), с которой тело движется. Рассмотрим следующее выражение: s(t) = sqrt(t) и v(t) = t² . Обе функции принимают значение 1 при t = 1: s(1) = 1 и v(1) = 1. Однако таблица значений показывает, что вблизи значения t = 1 функции изменяются по-разному.
| t | s(t) | v(t) |
| 0,8 | 0,8944 | 0,64 |
| 0,9 | 0,9486 | 0,81 |
| 1 | 1 | 1 |
| 1,1 | 1,0488 | 1,21 |
| 1,2 | 1,0954 | 1,44 |
Видно, что функция v меняется сильнее, чем функция s. Чтобы определить это изменение – то есть определить производную, – возьмем некоторое число а и число а + h и сравним, как изменяются разности ƒ(a + h) – ƒ(a), с одной стороны, и a + h – а = h, с другой стороны. Затем определим частное:
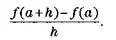
Используя формулы функций s(t) = sqrt(t) и v (t) = t² , определим значение частного при а = 1 и различных значениях h.
| h | s(1+h)-s(1)/h | v(1+h)-v(1)/h |
| -0,01 | 0,5012 | 1,99 |
| -0,001 | 0,5001 | 1,999 |
| 0,001 | 0,4998 | 2,001 |
| 0,01 | 0,4987 | 2,01 |
Результат для функции v близок к 2, в то время как для функции s – около 0,5, и это подтверждает данные первой таблицы, где мы заметили, что функция v менялась сильнее, чем функция s. Теперь нас интересует значение частного
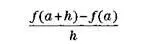
при h = 0, то есть когда а + h совпадает с a. Это значение мы назовем производной ƒ в точке а и, вслед за математиком Жозефом Луи Лагранжем (1736-1813), обозначим его ƒ'(a). Как можно убедиться, результат вычислений будет равен 0/0, то есть не имеет смысла.
Однако этот результат лишь кажется абсурдным, поскольку, как показывает предыдущая таблица для наших функций s(t) = sqrt(t) и v(t) = t² , когда h – маленькое число, хотя и стремящееся к нулю, оба частных,
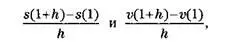
вполне имеют смысл и похожи на уже полученные значения: 0,5 для функции s(t) = sqrt(t), и 2 – для функции v(t) = t². Немного дальше мы увидим, что на самом деле эти значения совпадают с производными обеих функций в точке 1: s'(1) = 0,5, v’(l) = 2.
Однако деление на ноль, с которым столкнулись при вычислении производной ученые XVII века, представляло некоторую сложность, которая появлялась каждый раз, когда они пытались вычислить, например, касательную к кривой или мгновенную скорость при известном расстоянии, пройденном движущимся телом.
Следует иметь в виду, что до появления анализа бесконечно малых (а произошло это в конце XVII века) могли изучаться только самые простые виды движения: равномерное движение, при котором пройденное расстояние линейно зависит от времени, скорость постоянна и отсутствует ускорение, или равномерно ускоренное движение, когда пройденное расстояние пропорционально квадрату времени и, таким образом, скорость пропорциональна времени и постоянному ускорению.
Изучение последнего вида движения, которое наблюдается, например, при падении тела под воздействием силы тяготения, потребовало всех мыслительных способностей гениального Галилея, который вник в сущность явления за несколько десятилетий до того, как благодаря анализу бесконечно малых изучение этого типа движения стало относительно простым.
Вернемся к одному из наших примеров: тело в движении прошло расстояние s(t) = sqrt(t) за время t (время мы измеряем в секундах, а расстояние – в метрах). Расчет средней скорости, с которой двигается тело, – задача легкая: например, за период времени между 1 и 4 секундами средняя скорость будет равняться результату деления пройденного расстояния на затраченное время:
Средняя скорость
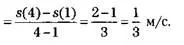
Но что произойдет, если вместо средней скорости за интервал времени мы захотим измерить мгновенную скорость, с которой движется тело в конкретный момент? Для простоты представим, что мы хотим измерить эту скорость именно в тот момент, когда наступает первая секунда движения. Для этого возьмем изменение времени h и посчитаем среднюю скорость между 1 и 1 + h.
Средняя скорость 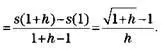
Чтобы посчитать мгновенную скорость в первую секунду, достаточно приравнять h к нулю. Но тогда, как и ранее, мы получим не имеющий смысла результат:
Мгновенная скорость в момент времени 1 = 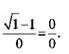
Это происходит потому, что мгновенная скорость соответствует значению производной функции, которая измеряет расстояние s(t) = sqrt(t) при t = 1.
Предыдущая таблица показывала, что значение этой производной должно быть 0,5. Теперь посмотрим как, используя предыдущее выражение, мы можем выполнить кажущееся бессмысленным деление на ноль и получить ожидаемое значение:
Средняя скорость 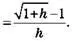
Далее умножаем числитель и знаменатель на sqrt(1+h) + 1 и сокращаем:
Средняя скорость 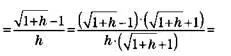
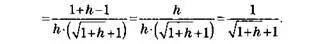
Если в этом выражении мы приравняем значение h к нулю, задача меняется, и при h = 0 отсутствует деление на ноль. Как и подсказывала таблица, частное при h = 0 составляет 0,5. В физических терминах это означает:
Мгновенная скорость в момент времени
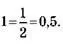
Таким образом, от бессмысленного деления нуля на ноль мы пришли к заключению, что если тело проходит sqrt(t) метров за t секунд, то за 1 секунду оно движется со скоростью:
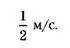
Другое базовое понятие анализа бесконечно малых – интеграл. Он применяется для измерения площади графика функции.
Пусть у нас есть функция ƒ, определенная между числами a и b, тогда интеграл . символ интеграл b a ƒ(t)dtесть площадь образованной функцией фигуры. Символ символ интегралдля записи интеграла ввел Лейбниц, он является стилизацией буквы s – первой буквы слова «сумма». Почему выбор Лейбница пал именно на нее, мы увидим позже.
Читать дальшеИнтервал:
Закладка:








