Феликс Филатов - Клеймо создателя

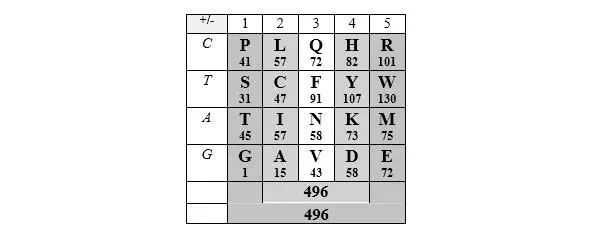
Общие нуклонные суммы симметричных пар столбцов 1-го и 3-го, 2-го и 4-го в матрице кода близки к равенству – или равны (176+320 = 118+378 = 496), если гистидин Н полностью протонирован (в версии «заряженной» матрицы), то есть имеет нуклонное число 82. Очень вероятно, что все это – не более, чем случайность, игра в цифры, – особенно если принимать во внимание, что 496 – единственное трехзначное (как и всякий кодон) совершенное число; выше мы уже отмечали это. Но продолжая эту игру, мы сталкиваемся с симметриями и соотношениями, которые озадачивают все больше. Зачем все это генетическому коду, «замороженной случайности», как назвал его Крик?

Приняв за случайность сам децимализм кода, на котором настаивает доктор Щербак, обнаруживаем, однако, что таблица кода в значениях нуклонных масс демонстрирует хорошо организованный набор информационных сигнатур 111 в системах счисления 5—9:

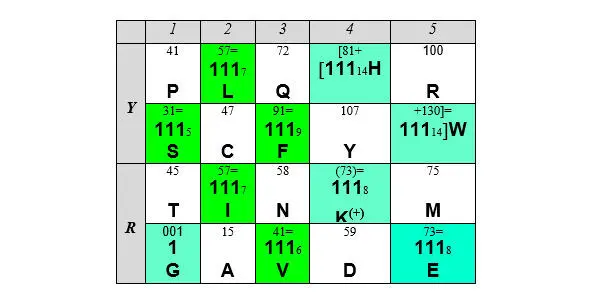
Ярко-зеленым в Таблице 11 отмечены ячейки тех аминокислот, нуклонная масса которых принимает значение 111 в той или иной системе счисления (номер системы счисления принято указывать справа и снизу от числа; номер десятичной системы не указывается). Бледно-зеленым отмечены ячейки тех аминокислот, нуклонная масса которых принимает значение 111 при определенных условиях: сложение нуклонных масс гистидина Н(81+) и триптофана W(+130) дает 211= 111 14 (других таких смежных пар в матрице нет), нуклонная масса лизина становится 111 8 в зарядовой версии этой аминокислоты, а нуклонная масса глицина – это базовый нумерал (цифровой символ) для подобных чисел. Сумма всех закрашенных ячеек матрицы кода составляет 777 9 .

Если скептически настроенный Читатель готов счесть всѐ это случайностью, обратимся на время к порядковым параметрам кодируемых аминокислот. В их значениях симетрии матрицы генетического кода приобретают такой вид:

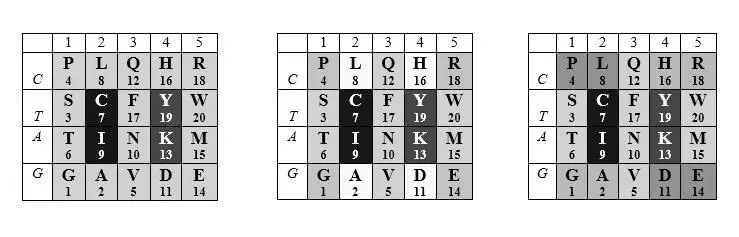
Все три таблицы практически одинаковы. В левой матрица состоит из двух блоков – PSTG\ RWMEи LQHF\NAVD, симметричных относительно центральной колонки (а также относительно границы между первыми кодонными пуринами и пиримидинами) и равновесных по суммам позиционных номеров (81=81), а также двух «внутренних» (неокрашенных) пар с соотношением сумм 1:2. В центральной эти два блока разделены на две симметричные части каждый ( PGREи LHAD; 37=37) и STWMи QFNV(44=44). В правой таблице попарно соединены «угловые» блоки PIDEи GAHR, симметричные по диагоналям – так что каждая четверка характеризуется суммой 37. В принципе все эти значения можно в какой-то мере, рассматривать, как указание на децимализм генетического кода, на который указывают числа 37 (37*3= 111 ) и «гомодублеты» 44 и 88. Читатель, возможно, найдет в матрице кода и другие симметрии.

Мы же попытались связать симметрии двумерной матрицы с симметриями трехмерного (объемного) тела, геометрическая симметрия которого задавалась бы по определению: в нашем случае, как мы об этом сказали выше, это простейшее платоново тело, тетраэдр. Нам хотелось найти тетраэдр, в котором формальное равновесие (например, равенство кооперативных нуклонных масс граней) сочеталось бы с равновесием по какой-либо из четко определенных функций, например, по принадлежности к синтетазному классу. Принципиально такая возможность возникает, если принять 20 кодируемых аминокислот с их числовыми параметрами за 20 равновеликих сфер-мономеров. Двадцать мономеров тетраэдра делятся на две структурообразующие группы:

инвариантные мономеры ( i ), т. е. мономеры вершин ( v ) и центров граней ( c ), взаимозамена которых сохраняет общую нуклонную массу граней, и

пара «внутренних» мономеров ( e ) каждого ребра, не входящих в группу ( i ).

Мы нашли, что весьма простое условие, а именно – зеркальная симметрия пар мономеров групп i (v, c) и e относительно оси матрицы, разделяющей первые пурины и пиримидины, при равенстве сумм нуклонных масс v и c и при размещении этих пар во всех четырех столбцах, позволяет сконструировать единственный тетраэдр, который, однако, характеризуется не полной, но билатеральной симметрией (нуклонным равновесием пар) граней при минимальном «размахе» по их нуклонным массам. Числовые значения этого равновесия в десятичной и в пятеричной системах счисления выражаются так:

(626+629 = 627+628) 10, или:

(10.00 1 +10.00 4 =10.00 2 +10.00 3 ) 5.

Пару i инвариантных мономеров составляют два мономера v и c , кодируемые одной и той же первой буквой, а пару е составляют внутренние мономеры ребра, также кодируемые одной и той же первой буквой; в обоих случаях используются все четыре основания. Поскольку у тетраэдра шесть пар е , а строк в матрице четыре, то две из этих пар (перекрещивающиеся), хотя и следуют указанному принципу, симметричны лишь в общем, пурин-пиримидиновом , формате – при условии принадлежности Sи Rк группе вырожденности II: T- R(кодирующие дублеты A C - A G ) и S- E(кодирующие дублеты AG - GA или R G - R A ). Поразительно, но этот простой принцип, иллюстрируемый приведенной ниже матрицей:

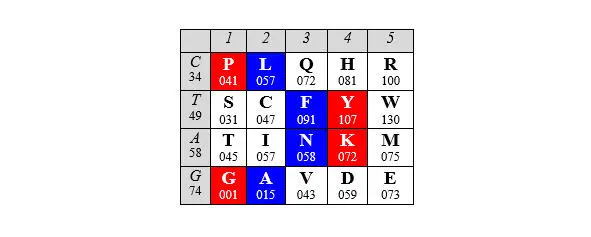
сводит число возможных версий трехмерной модели кода к единственной:

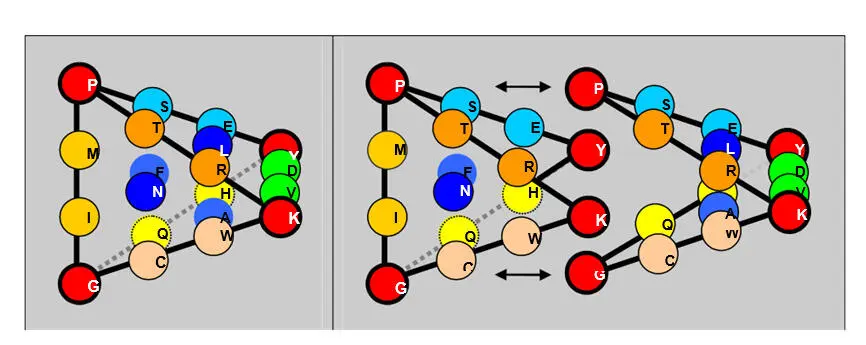
Правда, равновесную по граням модель можно также построить, заменив ребра QHи VDна QVи НDи сохранив, таким образом, симметричный рисунок реберных мономеров в составе матрицы, однако, эта версия потребует сделать формулировку принципа сборки тетраэдра более свободной, поскольку наш тетраэдр характеризуется также полной симметрией по граням аминокислот двух арс-классов:на каждую его грань приходится равное (по 5) число мономеров-аминокислот каждого класса.