Феликс Филатов - Клеймо создателя

Рассмотрим подробнее еще одну таблицу кода 6060 61, основанную на совершенно иных принципах. Щербаком она приводится в виде кольца и иллюстрирует «общий естественный баланс универсального генетического кода». Мы, однако, представляем эту таблицу в виде линейной последовательности, поскольку «кольцевой пептид» – да еще такой длины в природе не встречается. Между тем, для нас важно выделить направление пептида, сохраняя и «конец», и «начало» внутри цепи. Константные части свободных аминокислот имеют массу 74, в то время, как в составе полипептида эта масса за счет поликонденсации снижается до 56. Вот почему мы представляем воображаемый минимальный полный пептид (МПП) генетического кода лишь как фрагмент некоего белка. Последовательность первых нуклеотидов является пермутацией упорядоченной по массе четверки ( CTAG ) – AGCT , сохраняющей исходную симметрию по комплементарности. Последовательность вторых нуклеотидов комплементарна (зеркально симметрична) последовательности первых: TCGA . Последовательность третьих нуклеотидов – пермутация последовательности вторых, но начинающаяся с пуринов ( GATC ) – в случае первых пуринов, и начинающаяся с пиримидинов ( TCGA ) – в случае первых пиримидинов. Именно такой порядок кодирующих МПП оснований соответствует реальному направлению кодирования – от стартового до терминирующего кодона:

В составе МПП пролин (выделен светло-серым) имеет реальные нуклонные массы своих частей – константной и вариабельной. Кроме того, в ней – как это имеет место в реальной клетке – полностью ионизированы аспарагиновая и глютаминовая кислоты и полностью протонированы аргинин и лизин. Что до гистидина, он в условиях клетки протонируется далеко не полностью, и его нуклонная масса остается в ней неизменной – 81.

Самой яркой чертой описываемого олигопептида является количественное равновесиенуклонных масс консервативных и вариабельных (боковых) частей составляющих его аминокислот: 3412 = 3412 . Между прочим, это равновесие – с небольшими отклонениями – воспроизводится практически для всех природных белков. В то же время для случайного набора аминокислот масса боковых цепочек превышает массу «хребта» из константных частей примерно на 12%.

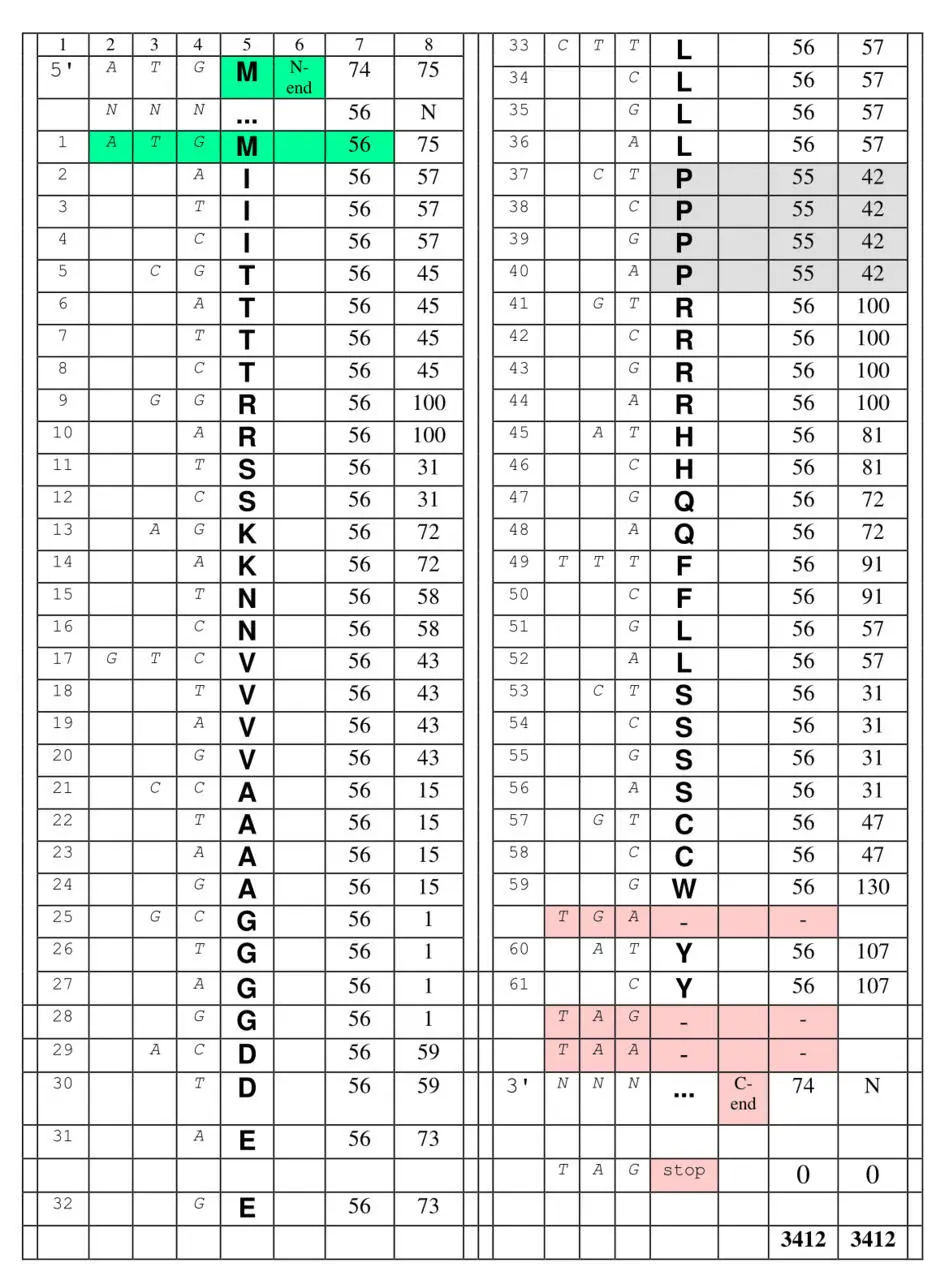
Может показаться, что эти числа, которыми выражаются общие и равные друг другу нуклонные массы боковых частей и стандартных блоков МПП (то есть результат оцифровки продуктов кодирования ), ничем не примечательны. Во всяком случае, они не имеют вида n 111 , который до сих пор привлекал наше внимание. Однако, номера нуклеотидов упорядоченных по нарастанию молекулярных масс C , то есть 1234 (рациональность чего – для первых кодонных оснований – мы показали в Главе А ), пермутированные в составе первых оснований, кодирующих МПП ( 3412 ), странным образом соответствуют нуклонным массам обеих частей этого пептида, выраженным в десятичной системе счисления: 3412 = 3412 = 3412 . В порядке ещѐ одного – математического курьеза отметим, что десятичное число 1234 в семеричной системе счисления записывается как 3412 7 .

Рациональная организация кодирующей последовательности может, таким образом, указывать на ведущую роль первых триплетных оснований в симметриях кода. Снова и снова указывает она и на базовую роль молекулярных масс в организации не только кодирующих правил, но также и кодируемого продукта. Кроме того, она показывает возможность оцифровки не только кодируемых (как у Щербака), но и кодирующих элементов – и не только в терминах нуклонных масс, но также используя простую нумерацию.

Удивительная организация генетического кода дает пищу великому множеству теоретиков и любителей для конструирования не только различного рода таблиц, но и объемных моделей. Большое количество разнообразных моделей кода можно отыскать в специальной и в не слишком специальной литературе. Автор не берется даже за краткий обзор результатов этой деятельности. Некоторые из них, на его вкус, как минимум, не интересны – например, попытка проводить параллели между организацией генетического кодирования и смысловым содержанием гексаграмм китайской Книги Перемен. В других он ничего не понимает – например, в топологической модели Владимира Карасева или в волновых моделях Петра Гаряева. В свое время Автор и сам оказался под некоторым впечатлением от трехмерной модели Трейнора и сотрудников – правда, потому только, что она представляла собой тетраэдр. Но модель строилась на основе кодирующих триплетов, а поскольку число их – 64 (не-тетраэдрическое), такой многогранник можно было построить только по определенным, не слишком логичным правилам. Гексаэдр (куб) годится для этой цели куда больше, поскольку 64=43, но он не так выразителен и опять-таки базируется на организации лишь одного из двух компонентов кода – азотистых оснований; кроме того, он уже практически использован в «обыкновенной» таблице генетического кода 4х4х4.

Некоторые модели остаются в тени или забыты совершенно незаслуженно. Например, объемная модель генетического кода Rafiki, Inc. , выполненная в виде игрушки (см. рисунок и развертку), могла бы, как минимум, использоваться на уроках биологии и будила бы воображение молодых людей, подогревая их интерес к этой науке и определяя и их, и ее будущее.

Эта игрушка представляет собой додекаэдр, «кристалл», собранный из 120 тетраэдров (Автор не вдается здесь в детали еѐ построения, их можно найти на сайте http://www.codefun.com/Index.htm). Разумеется, ничего подобного в природе нет, зато модель Рафики хорошо иллюстрирует симметрии кодирования и даже некоторые аспекты укладки белковых молекул.

Между тем число продуктов кодирования (20) дает соблазн собрать именно тетраэдр; надо только сформулировать простой принцип сборки, желательно учитывающий и кодирующие основания, и кодируемые аминокислоты, помня об упомянутом выше ограничении Эйгена: теория может быть корректной или нет; модель имеет третью возможность – оставаясь корректной, совершенно не относиться к делу (a theory has only the alternative of being wrong; a model has a third possibility – it might be right but irrelevant