Владимир Живетин - Человеческий риск (системные основы управления)

Человеческий риск будем оценивать величиной вероятности выхода фактической модели состояния динамической системы, в том числе динамической биосистемы – человека, из области допустимых состояний. Таким образом, мы хотим выделить те ситуации, которые ведут к потерям, т. е. связаны с риском. Для анализа процесса жизнедеятельности введем гипотезы В 1и В 2.

Гипотеза В 1 . Фактическое состояние динамической системы, характеризуемое моделью F ф , находится в области допустимых состояний, т. е. F ф 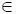Ω доп .

Гипотеза В 2 . Хотя бы один объект-подсистема динамической системы имеет фактическое состояние, которое находится вне допустимой области, т. е. F ф 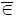Ω доп .

При этих двух гипотезах динамическая система с помощью системы контроля формирует две модели А 1и А 2, представленные в виде двух сигналов-событий:

А 1 = { F k 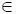Ω o доп } , А 2 = { F k 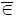Ω o доп }.

Ситуация, когда справедлива гипотеза В 1и выполняется событие А 1, соответствует такому функционированию человека и используемых им систем контроля, при которых цель жизнедеятельности выполняется, т. е. нет потерь, нет риска. Вероятность пересечения этих событий обозначим через Р 1 = Р ( В 1 ∩ А 1).

В случае когда реализуются гипотеза В 1и событие А 2, у человека создается ложное представление (оценка) о состоянии динамической системы, и эта оценка создается по причине возникновения погрешности δ F . Вероятность такого события Р 2= Р ( В 1 ∩ А 2).

Событие В 2 ∩ А 1означает, что фактическое состояние контролируемого объекта находится вне области допустимых состояний, риск велик, а концептуальная модель F к указывает человеку, что все в порядке, и динамическая система достигает цель, риска нет. Обозначим вероятность этого события Р 3 = ( В 2∩ А 1) как вероятность часто реализуемой ситуации риска.

Рассмотрим гипотезу В 2и событие А 2. Эта ситуация соответствует такому состоянию динамической системы, в том числе человека, при котором цель жизнедеятельности не выполняется, так как фактическое значение F находится вне области допустимых состояний. Такая ситуация обусловлена как ошибками самого человека δ 1 F, так и неопределенностью внешней информации δ 2 F. Вероятность этого события обозначим Р 4 = Р ( В 2∩ А 2).

Рассматриваемые события образуют полную группу несовместных событий, и поэтому 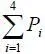= 1. С целью упрощения дальнейших выкладок, учитывая сказанное выше, поставим в соответствие: модели F ф процесс x ф ; модели F к процесс x изм , когда модели F ф соответствует вектор фактических параметров состояния x ф ( t ), модели F к соответствует вектор измеренных x изм ( t ) или оценочных состояний. На рис. 1.8 представлена диаграмма событий В i , A j ( i = 1,2; j = 1,2) для случая, когда на х накладывается ограничение сверху, т. е. область допустимых значений х должна быть меньше x в д оп .

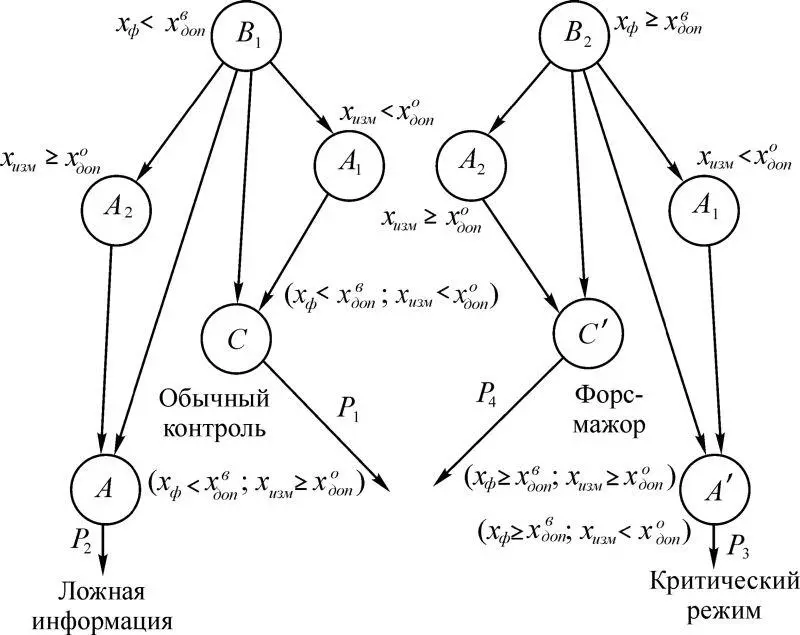
Рис. 1.8

Для решения задачи анализа необходимо установить связь между вероятностями Р i 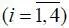, допустимыми значениями векторов x ф , x изм , а также плотностями вероятностей векторов x ф и x изм . С этой целью, учитывая определения,

В 1 = { x ф ( t ) 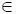Ω доп 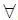( t ) t 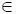| t 0, T ]}, В 2 = { x ф ( t ) 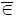Ω доп 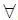( t ) t 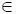| t 0, T ]},

A 1 = { х изм ( t ) 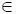Ω пр доп 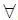( t ) t 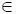| t 0, T ]}, A 2 = { х изм ( t ) 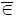Ω пр доп 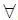( t ) t 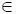| t 0, T ]},

представим рассматриваемые вероятности в виде:

Р 1 = Р {[ x ф ( t ) 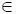Ω доп ( t )] ∩ [ х изм ( t ) 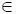Ω пр доп ( t )]},

Р 2 = Р {[ x ф ( t ) 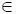Ω доп ( t )] ∩ [ х изм ( t ) 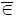Ω пр доп ( t )]},

Р 3= Р {[ x ф ( t ) 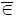Ω доп ( t )] ∩ [ х и зм ( t ) 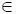Ω пр доп ( t )]};

Р 4 = Р {[ x ф ( t ) 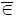Ω доп ( t )] ∩ [ х изм ( t ) 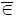Ω пр доп ( t )]}.

При этом риск характеризуется векторной величиной P = ( P 2, P 3 , P 4), включающей в себя вероятности P 2 , P 3, обусловленные погрешностями оценки, и вероятность P 4, обусловленную одновременно выходом х ф из области Ω доп и х о из Ω o доп .

В дальнейшем будем предполагать, что множества из Ω доп , Ω о доп образуют односвязные области ω доп и ω о доп соответственно. Тогда для искомых вероятностей получим:

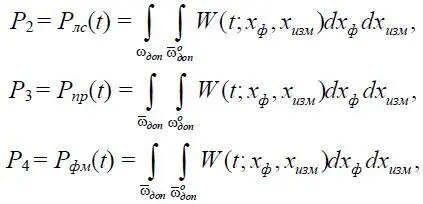
где W ( t ; x ф, x изм ) – совместная плотность вероятности компонент-векторов x ф и х изм в момент времени t; 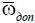, 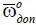– области, образованные множествами 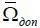, , 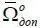которые представляют собой дополнения к Ω доп , Ω о доп .