Владимир Живетин - Человеческий риск (системные основы управления)

6. Цель может достигаться при различных сочетаниях значений вектора x = ( 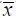, y, z ) из области допустимых значений путем управления параметрами ( у, z ).

7. Каждая динамическая система имеет область критических состояний Ω кр , в которой она теряет свои свойства и неспособна выполнять поставленные цели.

Все х 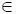Ω кр обозначим через х кр . В результате потери, обусловленные невыполнением цели, связаны с выходом ограничиваемых параметров х в критическую область.

8. Все те значения х , при которых динамическая система способна выполнять свое функциональное назначение, назовем допустимыми и обозначим х доп . Все значения х доп образуют некоторое открытое множество, которое обозначим Ω доп .

9. Величина Δ 1 = ( х кр – х доп ) представляет собой запас на неблагоприятные сочетания случайных факторов, влияние которых на процесс функционирования динамической системы невозможно оценить в каждой конкретной ситуации.

10. Область допустимых состояний Ω доп и соответствующие ей х доп изменяются в процессе функционирования динамической системы и определяются экспериментально или теоретически [18].

11. Для предотвращения потерь и наилучшего достижения цели динамическая система имеет системы контроля и управления [17].

С помощью систем контроля, обладающих погрешностями, в процессе функционирования динамической системы вычисляют (строят) Ω* доп . При этом, как правило, Ω доп не совпадает с Ω* доп за счет погрешностей функционирования систем контроля.

12. Человек для управления использует измеренные значения контролируемых параметров, которые обозначим х изм .

13. На выходе динамической системы реализуются текущие или фактические значения параметров, которые обозначим х ф . При этом х изм = х ф + δ х, где δ х – погрешность измерения – в общем случае случайный векторный процесс.

14. Фактические значения параметров х ф в силу объективных причин, обусловленных внешними возмущениями и внутренними факторами риска (шумами), а также свойствами оператора-человека, изменяющимися случайным образом, представляют собой случайные процессы. На этапе проектирования динамической системы векторный процесс х ф определяется с помощью математических моделей.

15. Для компенсации влияния δ х на величину риска вводятся допустимые оценочные значения параметров х o доп и соответствующая им область Ω o доп 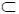Ω доп , т. е. вводится запас Δ = ( х доп – х o доп ). При контроле динамических процессов, когда скорость изменения процесса во времени 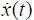≠ 0, необходимо вводить дополнительный запас 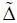= k | 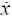| и вектор х дин доп = х доп ± 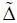. В результате имеем Ω o доп 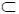Ω дин доп 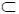Ω доп , т. е. х o доп ≤ х дин доп ≤ х доп .

16. Предотвращение потерь состоит в обеспечении условия х ф ( t ) 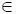Ω доп ( t ) для любого момента времени t функционирования динамической системы. Для целей управления оператор имеет х изм , кроме того, система контроля индуцирует оператору не Ω доп , а Ω* доп . При этом х * доп = х доп + δ х доп , где δ х доп – погрешность функционирования системы контроля, х * доп 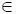Ω* доп . В этих условиях оператор может обеспечить только х изм 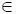Ω* доп , а это означает, что возможен выход х ф из области Ω доп , что означает соответствующие потери и риск.

17. В силу того что процессы х ф и х изм являются случайными, в качестве меры риска будем рассматривать вероятности Р i 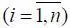событий, приводящих к различным потерям человеческой деятельности.

18. С учетом сказанного необходимо разработать показатели риска

Р i= Р i (Ω доп , Ω дин доп , Ω o доп , М ф k ( x ф ), М 0 k ( x изм ), а, b ) ,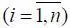

где М ф k ( x ф ) – момент k-го порядка случайного векторного процесса х ф; М 0 k ( x изм ) – момент k -го порядка случайного векторного процесса х изм ; а, b – параметры системы, векторные величины.

19. В дальнейшем под человеческим риском будем понимать вероятность неадекватного отображения окружающей среды, в результате чего параметры х i , подлежащие контролю и ограничению, принимают значения х i 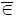Ω доп , т. е. принадлежат критической области.

20. Полученные расчетным путем Р i 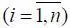уточняются в процессе функционирования динамической системы. В последнем случае уточняются как Р i , так и область Ω o доп .

Человек оперирует с концептуальной моделью F k объекта контроля, представляющего собой динамическую систему. В среде жизнедеятельности имеет место фактическое состояние динамической системы, которому соответствует модель F ф . При этом имеем F k = F ф + δ F. В общем случае F ф представляет собой модель всей динамической системы, состояние которой характеризуется совокупностью параметров x ф ( t ). В частном случае это может быть одна из компонент вектора x ф ( t ), т. е. ( x i ) ф .

Переход от модели F ф к вектору x ф часто приближенно отображает реальный мир, реальные объекты. Однако, как правило, такой переход необходим, т. к. только в этом случае мы сможем численно оценить искомую величину.

Так, у шофера при обгоне отображается полная модель дорожной ситуации: десятки машин (на дороге, обочине), люди. Однако из этой полной модели он выделяет только один объект, его скорость V и расстояние l до него, это именно тот объект, с которым он может столкнуться. При этом модель F ф с распределенными в пространстве и во времени n объектами заменяется моделью F ф ( x ) с одним объектом, состояние которого характеризуется двумя параметрами: х 1= V; х 2= l. При этом x = ( х 1, х 2).