Александр Казанский - Дискретная математика. Краткий курс. Учебное пособие

Рассмотрим пример. Пусть имеется разбиение множества U , показанное на рис. 1.10. Выделим множество, которое задается формулой (нормальной формой объединения пересечений) А ∪ ( В С ∩ С ). Она задает объединение двух множеств: А = {4, 5, 6, 7} и множества, представляющего собой пересечение множеств В С и С , т. е. множества В С ∩ С = {1, 5}. Поэтому множество А ∪ ( В С ∩ С ) = {1, 4, 5, 6, 7}. На рис. 1.12 это множество заштриховано. Из диаграммы видно, что множество А ∪ ( В С ∩ С ) задается объединением пяти фундаментальных произведений: множеству {4} соответствует фундаментальное произведение А ∩ В С ∩ С С, множеству {6} – А ∩ В ∩ С С, множеству {7} – А ∩ В ∩ С , множеству {5} – А ∩ ВC ∩ С и множеству {1} – АC ∩ ВС ∩ С. Объединение этих фундаментальных произведений и дает полную нормальную форму

( А ∩ В С ∩ С С) ∪ ( А ∩ В ∩ С С) ∪ ( А ∩ В ∩ С ) ∪ ( А ∩ В С ∩ ∩ С ) ∪ ( А С ∩ В С ∩ С ).

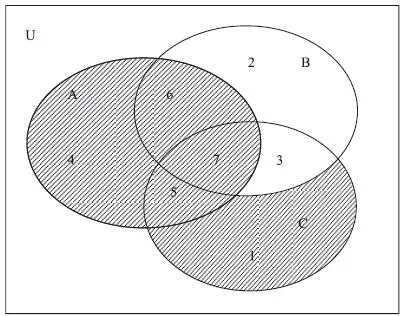
Рис. 1.12

Заметим, что для любого множества существует не только единственная полная нормальная форма объединения пересечений, но и единственная полная нормальная форма пресечения объединений. Эту форму также можно найти двумя способами. Так, для множества из предыдущего примера А ∪ ( В С ∩ С ) раскроем скобки и получим выражение в нормальной форме пересечения объединений ( А ∪ В С) ∩ ( А ∪ С ). В первой скобке нет переменной С , а во второй переменной В. Поскольку выражение ( С ∩ С С) = Ø , то следующее выражение эквивалентно исходному

(( А ∪ В С) ∪ ( С ∩ С С)) ∩ (( А ∪ С ) ∪ ( В ∩ В С)) = ( А ∪ В С ∪ С ) ∩ ( А ∪ В С ∪ С С) ∩ ( А ∪ В ∪ С ) ∩ ( А ∪ В С ∪ С ) = ( А ∪ В С ∪ С ) ∩ ( А ∪ В С ∪ С С) ∩ ( А ∪ В ∪ С ).

Последнее выражение и будет полной нормальной формой пересечения объединений для исходной формулы.

Найти данное выражение можно также и при помощи диаграммы Венна. Поскольку в исходное множество {1, 4, 5, 6, 7} не вошли элементы {0, 2, 3 }, то необходимо образовать пересечение таких объединений, которые не содержат эти три множества. Объединение А ∪ В ∪ С не содержит элемента {0}, объединение А ∪ В С ∪ С не содержит элемента {2} и объединение А ∪ В С ∪ С С не содержит элемента {3}. Отсюда, образовав из них пересечение, можно получить полную нормальную форму пересечения объединений

( А ∪ В ∪ С ) ∩ ( А ∪ В С ∪ С ) ∩ ( А ∪ В С ∪ С С).

Более подробно эти формы будут рассмотрены в упражнениях.

Множество можно задавать различными формулами. Хотя эти формулы выглядят по-разному, но все они эквивалентны в том смысле, что они определяют одни и те же элементы данного множества. Например, пусть имеются два выражения в нормальной форме:

Е1 = ( В ∩ С ) ∪ ( А С ∩ С С),

Е2 = ( В ∩ С ) ∪ ( А С ∩ В ) ∪ ( А С ∩ В С ∩ С С).

Эти формулы эквивалентны, что нетрудно проверить, если преобразовать каждую из них к полной нормальной форме, которая и для Е1 и для Е2 одна и та же:

( А ∩ В ∩ С ) ∪ ( А С ∩ В ∩ С ) ∪ ( А С ∩ В ∩ С С) ∪ ( А С ∩ В С ∩ С С).

Для того чтобы определить, какая из эквивалентных формул «проще», введем следующие обозначения. Пусть Е – выражение в нормальной форме и пусть L ( E ) – количество литералов в этом выражении (считаются все вхождения) и F ( E ) – количество произведений, из которых образовано Е . Так, для Е 1 значение L ( E 1) = 2 + 2 = 4 и F ( E 1) = 2, а L ( Е 2) = 2 + 2 + 3 = 7 и F ( E 2) = 3.

Пусть Е1 и Е2 эквивалентные выражения в нормальной форме. Тогда Е1 проще Е2 если

L ( E 1) < L ( Е 2) и F ( E 1) < L ( Е 2) или

L ( E 1) < L ( Е 2) и F ( E 1) < L ( Е 2).

Выражение Е , представленное в нормальной форме, называется минимальным, если не существует никакого другого эквивалентного ему выражения, которое проще, чем Е . Следует заметить, что может существовать более одного эквивалентного минимального выражения.

Произведение Р называется простым импликантом, для выражения Е , если

Р ∪ Е = Е

и нет никакого другого произведения, содержащегося в Р, которое обладает этим свойством. Например, пусть

Е = ( А ∩ С ) ∪ ( В С ∩ С ) ∪ ( А С ∩ В ∩ С ).

Можно показать, что выражение

( А С ∩ В ) ∪ Е = Е , но А С ∪ Е ≠ Е и В ∪ Е ≠ Е .

Поэтому А С ∩ В является простым импликантом Е .

Теорема 1.3. Любое выражение Е , представленное в минимальной форме, является объединение простых импликантов Е .

Методы определения минимальных форм обычно базируются на алгоритмах, которые позволяют находить простых импликантов и выбирать из них те, которые и дают выражения в минимальной форме. Для определения простых импликантов имеется метод соседства (его также называют методом консенсуса), который состоит в следующем. Пусть P i и P j – такие два произведения, что одно из них содержит литерал Х , а другое Х С (т. е. какая-то переменная в одно произведение входит без дополнения, а в другое с дополнением и других переменных с этим свойством в данных произведениях нет). Тогда соседством P i и P j будет называться произведение (без повторений), составленное из литералов P i и P j, из которых удалены Х и Х С, а сами P i и P j называются соседними. Соседство не определено, если P i = X и P j = X C.

Из определения соседства следует следующее утверждение:

если S является соседством Pi и Pj , то тогда

P i ∪ P j ∪ S = P i ∪ P j.

Пример 1.9.Найти соседство S для P 1 и Р 2.

1) P 1 = ( А ∩ В ) и Р 2 = ( В С ∩ С С), удалим В и В С и образуем пересечение P 1 и Р 2 получим S = А ∩ С С.

2) P 1 = А С ∩ В С ∩ С и Р 2 = В С ∩ С С, удалим С и С С, получим без повторений S = А С ∩ В С.

3) P 1 = В и Р 2 = В С ∩ С С, удаление В и В С дает S = С С.

4) P 1 = А С ∩ В С ∩ С и Р 2 = В ∩ С ∩ D , удаление В С и В дает S = А С ∩ С ∩ D .