Александр Казанский - Дискретная математика. Краткий курс. Учебное пособие

– список студентов, которые не имеют пропусков по математике и английскому языку, но имеют – по информатике, A С ∩ B ∩ C С = {8};

– список студентов, которые не имеют пропусков по математике, но имеют по информатике и английскому языку, A С ∩ B ∩ C = Ø ;

– список студентов, которые имеют пропуски по математике, но не имеют по информатике и английскому языку, ( A ∩ B С ∩ C С) = {1,6};

– список студентов, которые имеют пропуски по математике и английскому языку, но не имеют по информатике, A ∩ B С ∩ C = {2,7};

– список студентов, которые не имеют пропусков ни по математике, ни по информатике, но имеют по английскому языку, A ∩ B ∩ C С = {3};

– список студентов, которые имеют пропуски по всем трем предметам, A ∩ B ∩ C = {4, 5}.

Получив эти данные, деканат хотел бы составить списки тех студентов, которые:

1) имеют пропуски по математике, но не имеют по информатике;

2) имеют пропуски по математике и информатике;

3) имеют по крайней мере один пропуск по математике.

Для того чтобы ответить на вопрос первого пункта, т. е. найти множество тех студентов, которые имеют пропуски по математике, но не имеют по информатике, надо составить многочлен из тех фундаментальных произведений, которые включают в себя множество A ∩ B С.Таких фундаментальных произведений два. Их объединение и дает искомый многочлен ( A ∩ B С ∩ C С) ∪ ( A ∩ B С ∩ C ) = {1, 6} ∪ {2, 7} = {1, 2, 6, 7}. Это легко доказать, если выполнить упрощение данной формулы:

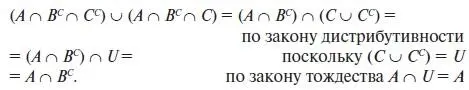
Аналогичное рассуждение можно применить и для второго пункта:

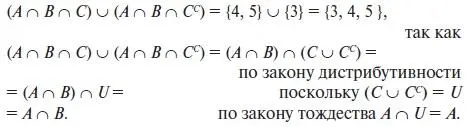
Для ответа на третий пункт, т. е. для определения множества А , надо составит многочлен из четырех фундаментальных произведений, содержащих множество А . Этот многочлен имеет вид

(A∩BС∩CС) ∪(A∩BС∩C)∪ (A∩B∩C) ∪(A∩B∩CC) = {1, 6}∪{2, 7}∪{3}∪{4, 5 } = {1, 2, 3, 4, 5, 6, 7}.

Многочлен можно упростить:

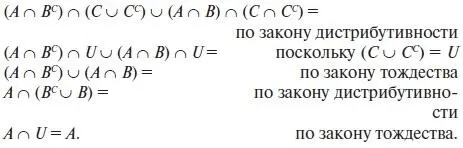
Решение задачи можно получить и при помощи диаграммы Венна, показанной на рис. 1.11.

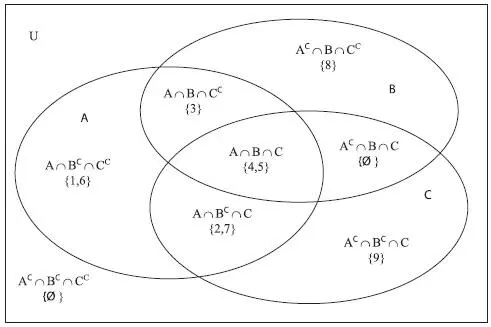
Рис. 1.11

Поскольку мы имеем все 8 комбинаций из трех исходных множеств и их дополнений, т. е. имеем все 8 фундаментальных произведений для трех множеств, то к решению данной задачи можно подойти и иначе. Допустим, нам надо выполнить первый пункт задачи, т. е. найти множество тех студентов, которые имеют пропуски по математике, но не имеют их по информатике. Фактически нам надо найти пересечение двух множеств: множества А (имеющих пропуски по математике) и множества В С (не имеющих пропусков по информатике), т. е. множество A ∩ B С. Для того чтобы найти элементы этого множества, нам нужно выразить множества A ∩ B С через фундаментальные произведения. Сделать это можно с помощью искусственного приема, который позволяет вводить в любое пересечение множеств те множества, которые в нем отсутствуют, приводя его тем самым к объединению фундаментальных произведений.

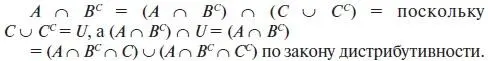
Это решение, по сути дела, представляет собой действия, произведенные при решении задачи в первом случае, но выполненные в обратном порядке. Это же способ позволяет выразить любое множество через фундаментальные произведения.

Множества с операциями пересечения, объединения и дополнения, удовлетворяющие абстрактным законам, введенным в главе 1, параграф 1.8, образуют алгебраическую систему, называемую алгеброй множеств. Эта алгебра является булевой алгеброй и поэтому часто использует идеи и терминологию булевой алгебры, однако следует отметить, что эта терминология не вполне стандартизирована, что иногда приводит к различным названиям одних и тех же понятий. Рассмотрим некоторые понятия более подробно.

Пусть имеется n переменных, каждая из которых определяет некоторое множество. Выражением алгебры множеств Е (или формулой) называется выражение, составленное из этих переменных, соединенных при помощи операций объединения, пересечения и дополнения, например

Е1 = A ∩ ( B С ∩ С )С ∪ ( A ∩ B С ∩ С C)С,

Е2 = A ∩ ( B С ∩ С ) ∪ ( A ∩ B С ∩ С C),

Е3 = ( A ∩ B С ∩ С ) ∪ ( A ∩ B С ∩ С C),

Е4 = ( A C ∪ B C) ∩ ( A C ∪ B C ∪ С ) ∩ ( B C ∪ С ),

Е5 = ( A C ∪ B ∪ С ) ∩ ( A ∪ B C ∪ С ) ∩ ( A C ∪ B C ∪ С )

являются выражениями из трех переменных А, В и С .

Литераломназывается переменная или дополнение переменной, например А, А С, В С и т. д. Произведениемназывается литерал или пересечение двух или более литералов, таких что ни одна пара из них не содержит одной и той же переменной. Например, B С ∩ С, A ∩ B С ∩ С C, А, С C являются произведениями, а выражения A ∩ B С ∩ А С и A ∩ B С ∩ B С – нет. Заметим, что любое пересечение литералов всегда приводится либо к Ø , либо к произведению. Так, например A ∩ B С ∩ А С = Ø , потому что A ∩ А С = Ø (по закону дополнения), а пересечение A ∩ B С ∩ B С = A ∩ B С, потому что B С ∩ B С = B С (по закону идемпотентности).

Если при n переменных произведение состоит из n литералов, то его называют фундаментальным произведением(некоторые авторы называют любое произведение фундаментальным произведением).

Выражение, представляющее собой объединение различных произведений, если в нем нет ни одного произведения, которое включается в другое произведение, называют суммой произведений, или нормальной формой объединения пересечений, или многочленом в нормальной форме. Из предыдущего примера Е1 является просто выражением, Е2 и Е3 – выражениями в нормальной форме объединения пересечений.

Если выражение состоит из объединения фундаментальных произведений, то такое выражение называют полной нормальной формой объединения пересечений, или многочленом в канонической форме. Многочлен Е3 кроме того, что он имеет нормальную форму объединения пересечений, является еще и многочленом имеющим полную нормальную форму объединения пересечений.