Александр Казанский - Дискретная математика. Краткий курс. Учебное пособие

Докажем законы поглощения.

A ∩ ( A ∪ B ) = A,

A ∪ ( A ∩ B ) = A .

Доказательство обоих законов очевидно. Пусть, например, x ∈ A ∩ ( А ∪ В ). Тогда мое x ∈ A и x ∈ ( А ∪ В ). Если допустить, что поскольку x принадлежит объединению А и В , то он принадлежит множеству В , но не принадлежит множеству А , но это приводит к противоречию, поскольку по определению пересечения x ∈ A . Другими словами, любой элемент левого множества может быть только из множества А .

Для доказательства закона де Моргана( A ∩ B )С = A C ∪ B C покажем сначала, что левое множество включается в правое ( A ∩ B ) С ⊆ A C ∪ B C. Пусть x ∈( A ∩ B )С. Тогда x ∉ A ∩ B . Из этого следует, что х не входит в оба множества одновременно, т. е. он не входит либо в А , либо в В. Если он не входит в А , то тогда он входит в А С, а если он не входит в В , то тогда он входит в В С. Отсюда следует, что х ∈ A C ∪ B C и поэтому ( A ∩ B ) С ⊆ A C ∪ B C.

Докажем теперь, что всякий элемент х из множества A C ∪ B C принадлежит и множеству ( A ∩ B )С. Если x ∈ A С, то тогда x ∉ A и поэтому х не может принадлежать пересечению x ∉ A ∩ B . Если x ∈ В С, то тогда x ∉ В и поэтому х также не может принадлежать пересечению x ∉ A ∩ B . В любом из этих случаев x ∉ A ∩ B и потому x ∈ ( A ∩ B )С.

Докажем двойственный закон де Моргана ( A ∪ B )C = = А C ∩ В C. Поскольку элемент х принадлежит множеству ( A ∪ B )C тогда и только тогда, когда он не принадлежит ни множеству А , ни множеству В , то из этого следует, что он должен входить и в множество А C, и в множество В C, т. е. в их пересечение А C ∩ В C. С другой стороны, если х входит в пересечение А C ∩ В C, то он не может входить ни в А , ни в В , потому что в пересечении дополнений множеств ни могут находиться элементы самих этих множеств. Но тогда х входит в дополнение к их объединению, т. е. x ∈ ( A ∪ B )С, что и требовалось доказать.

Доказательство закона инволюции( A C)C = A следует из того факта, что любой элемент из U принадлежит либо А , либо A C. Поэтому когда берется дополнение к множеству А , то получается множество А С, а когда берется дополнение к А С, то снова получается множество А .

Законы дополнения и тождества очевидны и не требуют доказательства.

Второй метод доказательства равенства тождеств состоит в использовании диаграмм Венна. Однако здесь иногда приходится рассматривать всевозможные случаи, при которых множества не имеют общих элементов, пересекаются или вкладываются друг в друга.

Докажем, например, закон де Моргана ( A ∩ B )С = A C ∪ B C. На рис. 1.9 представлены три случая: (а) когда А и В не пересекаются, (b) когда А включается в В и (с) когда в пересечение входят элементы и из А, и из В (имеется и случай, когда В включается в А , но он аналогичен случаю (b)). На рис. 1.9 (d), (e) и (f) показаны их дополнения. Далее на (а1), (b1) и (с1) показаны множества ( A C ∪ B C) для каждого из этих случаев. Можно видеть, что на каждом рисунке области для множества ( A ∩ B )С и множества ( A C ∪ B C) одинаковые во всех трех случаях и поэтому эти множества равны.

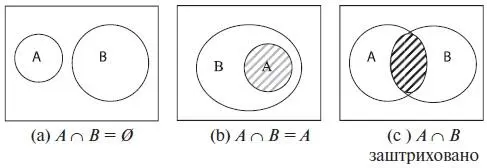
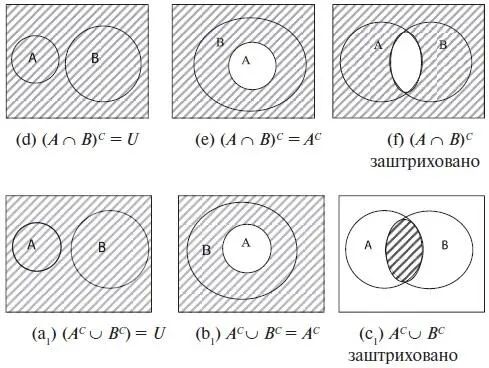
Рис. 1.9

Рассмотрим табличный методдоказательства равенства множеств. Докажем ассоциативность пересечения ( A ∩ B ) ∩ C = A ∩ ( B ∩ C ). Пусть имеется диаграмма Венна для трех множеств A, B и С из универсального множества U на рис. 1.10. Три овальные области представляют собой множества A, B и С . Прямоугольная область определяет множество U , и она разбита на восемь областей, которые помечены цифрами от 0 до 7. Можно видеть, что область разбиения 7 определяет множество A ∩ B ∩ C, область 6 – множество A ∩ B ∩ C С и т. д. Чтобы по диаграмме Венна проверить ассоциативность пересечения, можно использовать следующую идею. Заменим множества A, B и С и их пересечения на соответствующие им множества из областей разбиения на этой диаграмме. Множество А заменяется на {4, 5, 6, 7}, В – на {2, 3, 6, 7} и С – на {1, 3, 5, 7}, A ∩ B – на {6, 7}, B ∩ C – на {3, 7}.

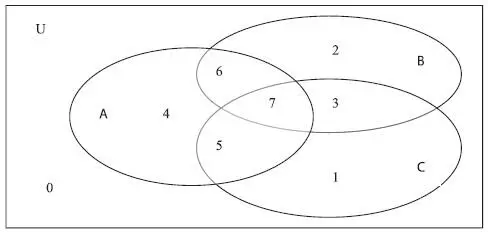
Рис. 1.10

Несмотря на то, что множества А, В и С могут быть какими угодно, доказать любое тождество для этих множеств можно, сведя доказательство к проверке этого тождества на уменьшенных множествах разбиения.

( A ∩ B ) ∩ C = A ∩ ( B ∩ C ),

{6, 7} ∩ {1, 3, 5, 7} = {4, 5, 6, 7} ∩ {3, 7}.

Нетрудно увидеть, что и левое, и правое множества этого тождества состоят из одного-единственного элемента 7, что и доказывает ассоциативность пересечения множеств.

Докажем то же самое используя табличный метод. Для этого построим таблицу, столбцы которой соответствуют различным множествам тождества, а каждая строка соответствует одному из множеств разбиения (строк 8, поскольку разбиение состоит из 8 множеств в соответствии с рис. 1.9). Строки содержат ответы на вопрос, входит ли соответствующее данной строке множество разбиения во множество доказываемого тождества или нет. Три первые столбца таблицы дают ответы, входит ли соответствующее множество разбиения во множество А , во множество В и во множество С . Столбец «Левая часть» соответствует левой части доказываемого тождества ( A ∩ B ) ∩ C , столбец «Правая часть» – правой части A ∩ ( B ∩ C ).

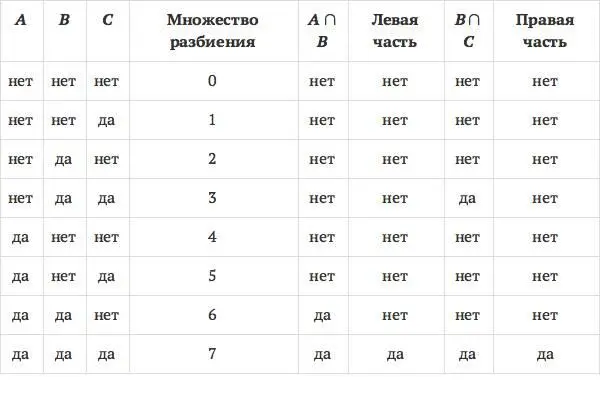
Поскольку ответы для всех строк «Левой части» те же самые, что и для «Правой части», тождество является доказанным. Табличный метод особенно удобен при построении доказательств с использованием компьютера.

Алгебраический методосновывается на идее разбиения доказательства на шаги, при этом переход от одного шага к следующему осуществляется за счет применения какого-либо закона алгебры множеств (например, закона ассоциативности, дистрибутивности, поглощения и т. д.). Доказательство требует хорошего знания базисных законов алгебры множеств, а также определенный опыт их применения. Рассмотрим метод на следующем примере. Пусть требуется доказать, что